操作与探究
我们知道：过任意一个三角形的三个顶点能作一个圆，探究过四边形四个顶点作圆的条件．
（1）分别测量图1、2、3各四边形的内角，如果过某个四边形的四个顶点能一个圆，那么其相对的两个角之间有什么关系？证明你的发现．

（2）如果过某个四边形的四个顶点不能一个圆，那么其相对的两个角之间有上面的关系吗？试结合图4、5的两个图说明其中的道理．（提示：考虑∠B+∠D与180°之间的关系）

由上面的探究，试归纳出判定过四边形的四个顶点能作一个圆的条件．

数轴是数与形和谐结合的桥梁，数轴在数学研究中有着非常重要的作用．华罗庚先生指出“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”．已知在纸面上有一数轴，数轴上有三个点，点A在点B的左边，点C表示的数是1．
（1）如果点A到原点的距离是3，点B到原点的距离是5．则点A和点B两点的距离是多少？
（2）如果点A到原点的距离是3，点B到点A的距离是5．则点B表示的数是多少？
（3）如果点A与点B到原点的距离相等，点A和点B之间的距离是2012．则点A、点B表示的数各是多少？
（4）如果点A与点B到点C的距离相等，点A和点B之间的距离是2012．则点A、点B表示的数各是多少？

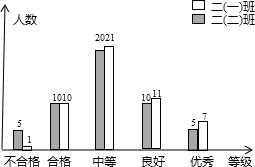
从A、B量水库向甲、乙两地调水，其中甲地需水15万吨，乙地需水13万吨，A、B两水库各调查水14万吨，从A地到甲地50千米，到乙地30千米；从B地到甲地60千米，到乙地50千米，设计一个调运方案使水的调运总量（单位：万吨•千米）尽可能小．
（1）设从A水库调往甲地的水量为x万吨，请你在下面表格空白处填上适当的数或式子．

地区 水库	甲	乙	总计
A	x	14-x 14-x	14
B	15-x 15-x	x-1 x-1	14
总计	15	13	28

（2）请你注意：影响水的调运量的因素有两个，即水量（单位：万吨）和运程（单位：千米），水的调运量是两者的乘积（单位：万吨•千米）．因此，从A到甲地有个调运量，从A到乙地也有个调运量：从B地…．设水的调运总量为y万吨•千米，则y与x的函数关系式y=（要求最简形式）
（3）对于（2）中y与x的函数关系式，若求自变量的取值范围，应该列不等式组：，解这个不等式组得：，据此，在给出的坐标系中画出这个函数的图象（不要求写作法）．
（4）结合函数解析式及其图象说明水的最佳调运方案，水的最小调运总量为多少？