(1 8分)近年来,我国始终不渝走和平发展道路,始终不渝奉行互利共赢的开放战略,始终不渝地维护我国国家利益。阅读材料,回答问题。
材料一 汇率战阴影未消,贸易战愁云又添。美国商务部于当地时间2011年11月9日的一纸公告,将价值近20亿美元、针对中国光伏产品的“双反(反倾销和反补贴)”案推至正式立案程序,相反却对在美国境内的相关企业加以补贴。这一贸易保护主义做法将严重影响到我国光伏产品对美国的出口。
(1)结合材料一,从《经济生活》角度说明我目光伏企业该如何扩大出口?(6分)
材料二 近期,有关南海问题不断出现新的复杂局面,就在东盟领导人会议召开前夕, 菲律宾高调宣布保卫南海,美国以多种形式介入南海问题。2011年11月18日,国务院总 理温家宝在会议上指出,中国将始终奉行“与邻为善,以邻为伴”的周边外交政策,目前南海存在的争议是多年积累下来的问题,应由直接有关的

主权国家通过友好协商和谈判予以解决,外部势力不应以任何借口介入。
(2)结合材料,说明温家宝总理的发言体现了我国外交政策的哪些具体

内容?(6分)
材料三2011年12月11日,联合国气候变化大会落下帷幕。会议各方显示了相当的政治诚意去推动气候谈判进程,致力于“拯救未来于当下”,坚持了双轨谈判机制,坚持了“共同但有区别的责任”原则,启动了绿色气候基金。但由于发达国家和发展中国家的分歧难以消弭,德班会议未能全部完成“巴厘路线图”谈判。
(3)在联合国气候变化大会上,与会各方取得积极成果但电存在难以消弭的分歧.这体 现了哪些《政治生活》道理?(6分)

 29、如图,已知点D、E为△ABC的边BC上两点.AD=AE,BD=CE,为了判断∠B与∠C的大小关系,请你填空完成下面的推理过程,并在空白括号内注明推理的依据.
29、如图,已知点D、E为△ABC的边BC上两点.AD=AE,BD=CE,为了判断∠B与∠C的大小关系,请你填空完成下面的推理过程,并在空白括号内注明推理的依据.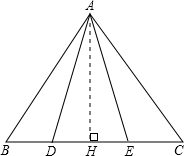
 主权国家通过友好协商和谈判予以解决,外部势力不应以任何借口介入。
主权国家通过友好协商和谈判予以解决,外部势力不应以任何借口介入。 内容?(6分)
内容?(6分)