
题目列表(包括答案和解析)
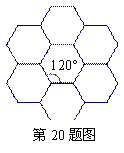
如图,蜂巢的横截面由正六边形组成,且能无限无缝隙拼接.称横截面图形由全等正多边形组成,且能无限无缝隙拼接的多边形具有同形结构.
若已知具有同形结构的正n边形的每个风角度数为a,满足∶360=ka(k为正整数),多这形外角和为360°,则k关于边数n的函数是________(写出n的取值范围即可).
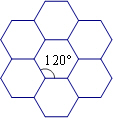
如图,蜂巢的横截面由正六边形组成,且能无限无缝隙拼接.称横截面图形由全等正多边形组成,且能无限无缝隙拼接的多边形具有同形结构.
若已知具有同形结构的正n边形的每个风角度数为![]() ,满足:360=k
,满足:360=k![]() (k为正整数),多这形外角和为360°,则k关于边数n的函数是 (写出n的取值范围即可).
(k为正整数),多这形外角和为360°,则k关于边数n的函数是 (写出n的取值范围即可).
 |
 95、小明、小敏两人一起做数学作业,小敏把题读到如图(1)所示,CD⊥AB,BE⊥AC时,还没把题读完,就说:“这题一定是求证∠B=∠C,也太容易了.”她的证法是:由CD⊥AB,BE⊥AC,得∠ADC=∠AEB=90°,公共角∠DAC=∠BAE,所以△DAC≌△EAB.由全等三角形的对应角相等得∠B=∠C.
95、小明、小敏两人一起做数学作业,小敏把题读到如图(1)所示,CD⊥AB,BE⊥AC时,还没把题读完,就说:“这题一定是求证∠B=∠C,也太容易了.”她的证法是:由CD⊥AB,BE⊥AC,得∠ADC=∠AEB=90°,公共角∠DAC=∠BAE,所以△DAC≌△EAB.由全等三角形的对应角相等得∠B=∠C. 24、如图,一块正方形地板由全等的正方形瓷砖铺成,这地板的两条对角线上的瓷砖全是黑色,其余的瓷砖是白色的,如果有101块黑色瓷砖,那么瓷砖的总数是多少.
24、如图,一块正方形地板由全等的正方形瓷砖铺成,这地板的两条对角线上的瓷砖全是黑色,其余的瓷砖是白色的,如果有101块黑色瓷砖,那么瓷砖的总数是多少.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com