
题目列表(包括答案和解析)
 8、已知:如图,在等边三角形ABC,AD=BE=CF,D,E,F不是各边的中点,AE,BF,CD分别交于P,M,N在每一组全等三角形中,有三个三角形全等,在图中全等三角形的组数是( )
8、已知:如图,在等边三角形ABC,AD=BE=CF,D,E,F不是各边的中点,AE,BF,CD分别交于P,M,N在每一组全等三角形中,有三个三角形全等,在图中全等三角形的组数是( ) 1、如图,已知图中有两对三角形全等,填空:
1、如图,已知图中有两对三角形全等,填空: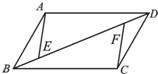 20、如图,平行四边形ABCD中,E、F是对角线BD上的点,且BE=DF.
20、如图,平行四边形ABCD中,E、F是对角线BD上的点,且BE=DF.



如图, ![]() 和
和![]() 均为等边三角形,连接BE、CD.
均为等边三角形,连接BE、CD.

1.(1)请判断:线段BE与CD的大小关系是 ;
2.(2)观察图,当![]() 和
和![]() 分别绕点A旋转时,BE、CD之间的大小关系是否会改变?
分别绕点A旋转时,BE、CD之间的大小关系是否会改变?

3.(3)观察图3和4,若四边形ABCD、DEFG都是正方形,猜想类似的结论是 ,在图4中证明你的猜想.

4.(4)这些结论可否推广到任意正多边形(不必证明),如图5,BB1与EE1的关系是 ;它们分别在哪两个全等三角形中 ;请在图6中标出较小的正六边形AB1C1D1E1F1的另五个顶点,连接图中哪两个顶点,能构造出两个全等三角形?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com