
题目列表(包括答案和解析)
如图,晚上小亮在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子( )
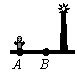
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短
晚上,人在马路上走过一盏路灯的过程中,其影子的长度的变化情况是
[ ]
如图所示,甲树通过以下变换,不能得到乙树的是
[ ]
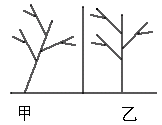
A.先轴对称,后平移,再旋转
B.先平移,后旋转,再轴对称
C.先旋转,后平移,再旋转
D.先旋转,后轴对称,再平移
 26、如图,晚上小亮在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子( )
26、如图,晚上小亮在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子( )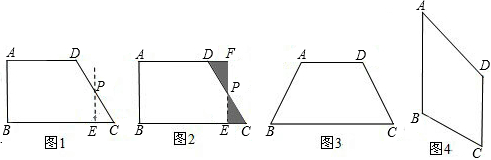
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com