在我们所学的课本中，多项式与多项式相称可以用几何图形的面积来表示，例如：（2a+b）（a+b）=2a²+3ab+b²就可以用下面图中的图①来表示．请你根据此方法写出图②中图形的面积所表示的代数恒等式：　　．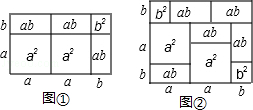

在我们所学的课本中，多项式与多项式相称可以用几何图形的面积来表示，例如：（2a+b）（a+b）=2a²+3ab+b²就可以用下面图中的图①来表示．请你根据此方法写出图②中图形的面积所表示的代数恒等式：　　．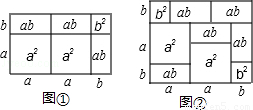

　　八年级甲班和乙班举行了一次联欢会．许刚在晚会上表演了一个小小的戏法．他从口袋里拿了一副扑克牌说：“这是一副普通的扑克牌，我要请一位同学将牌洗均匀，谁来洗？”陈逸上来接过牌，啪啪啪地洗了几次，交给许刚．许刚随即将牌装进了口袋说：“牌已洗匀了，现在请一位同学随便报一个不大于15的正整数，我总能抽出一组牌，其数值相加正好是你所报的数．”大家的脸上显示出了困惑的表情，真有这么神吗？花卉报了一个“14”，许刚立即从口袋里的牌中抽出一组牌，摊放在桌上，大家一看是2，4，8这三张牌，它们的和正好是14．报了几个数，许刚的表现都正确无误，难道许刚真的会魔法吗？

　　当然，魔法是不存在的，但这戏法的奥妙在哪里呢？你能揭穿它吗？

　　这个戏法的最关键之处是要构造一组数，使得15以内的正整数都能用这组数中的几个数的和来表示．这组数是2的连续次幂，即1，2，4，8，不超过15的正整数都可以用以上4个数中的几个或全部的和来表示．你不妨验证一下．

　　许刚在做戏法前已抽出了以上的4张牌，并将它们按顺序叠好先放置在口袋里．当他叫陈逸洗牌时，因为整个一副牌里只少了4张牌，谁也不会在意的．然后他将洗好的牌放进口袋，将事先选取的4张牌叠放在整副牌的上面．这样当然可以不费力地抽出需要的几张．

若要求所报的数不超过31，你会设计吗？你应如何表演呢(注：扑克牌里找不到16点，你可用K和3代替)？