练习册

  • 练习册
  • 试题
    15．若由(a+1)x=a+1得到x=1,则a= . 【查看更多】

     

    题目列表(包括答案和解析)

    由多项式的乘法法则知：若（x+a）（x+b）=x2+x+q，则p=a+b，q=a·b；反过来x2+x+q=（x+a）（x+b）要将多项式x2+x+q进行分解，关键是找到两个数a、b，使a+b=p，a·b=q，如对多项式x2-3x+2，有p=-3，q=2，a=-1，b=-2。此时（-1）+（-2）=-3，（-1）（-2）=2，所以x2-3x+2可分解为（x-1）（x-2）即x2-3x-2=（x-1）（x-2）。
    （1）根据以上填写下表：
    多项式
    p
    q
    a
    b
    分解结果
    x2+9x+20
     
     
     
     
     
    x2-9x+20
     
     
     
     
     
    x2+x-20
     
     
     
     
     
    x2-x-20
     
     
     
     
    （2）根据填表，还可得出如下结论：
    当q是正数时，应分解成两个因数a、b_______________号，a、b的符号与__________相同；
    当q是负数时，应分解成的两个因数a、b______________号，a、b中绝对值较大的因数的符号与_______相同。
    （3）分解因式：
    x2-x-12=_____________；x2-7x+6=________________。

    查看答案和解析>>

    由两个人玩抢10的游戏，游戏规则是这样的：第一个先说1或1、2，第二个人要接着往下说一个或两个数，然后轮到第一个人，再接着往下说一个或两个数，这样两人反复轮流，每次每人说一个或两个数都可以，但不可以连说3个数，谁先抢到10，谁就得胜。
    （1）你认为这个游戏公平吗？若不公平，它偏向哪个报数的人？
    （2）让你先说，你有必胜的把握吗？说出你获胜的策略。

    查看答案和解析>>

    有两个可以自由转动的均匀转盘A，B都被分成了3等份，并在每一份内均标有数字，如图所示，规则如下：①分别转动转盘；②两个转盘停止后观察两个指针所指份内的数字（若指针停在等份线上，那么重转一次，直到指针指向某一份内为止）。

    （1）用列表法（或树状图）分别求出“两个指针所指的数字都是方程x2-5x+6=0的解”的概率和“两个指针所指的数字都不是方程x2-5x+6=0的解”的概率；
    （2）王磊和张浩想用这两个转盘作游戏，他们规定：若“两个指针所指的数字都是x2-5x+6=0的解”时，王磊得1分；若“两个指针所指的数字都不是x2-5x+6=0的解”时，张浩得3分，这个游戏公平吗？若认为不公平，请修改得分规定，使游戏对双方公平。

    查看答案和解析>>

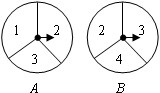
    有两个可以自由转动的均匀转盘A、B被分成了3等份，并在每份内均标有数字，如图所示，规则如下：①分别转动转盘A、B；②两个转盘停止后，将两个指针所指份内的数字相乘（若指针在等分线上，那么重转一次，直到指针指向某一份为止）.

    （1）用列表法(或树形图)分别求出数字之积为3的倍数和数字之积为5的倍数的概率；

    （2）小明和小亮想用两个转盘做游戏，他们规定：数字之积为3的倍数时，小明得2分；数字之积为5的倍数时，小亮得3分，这个游戏对双方公平吗？请说明理由；以为不公平的，试修改得分规定，使游戏对双方公平。

    查看答案和解析>>

    李明和张强两位同学为得到一张观看足球比赛的入场券，各自设计了一种方案：
    张强：如图，设计了一个可以自由转动的转盘，随意转动转盘，当指针指向阴影区域时，张强得到了入场券；否则，李明得到入场券；
    李明：将三个完全相同的小球分别标上数字1、2、3后，放入一个不透明的袋子中。从中随机取出一个小球，然后放回袋子；混合均匀后，再随机取出一个小球。若两次取出的小球上的数字之和为奇数，张强得到入场券；否则，李明得到入场券。
    请你运用所学的概率知识，分析张强和李明的设计方案对双方是否公平。

    查看答案和解析>>


    同步练习册答案