题目列表(包括答案和解析)
代数式
的系数是 ，代数式1－2x是 与 这二项的和。
代数式axy2－
x与2x－bxy2的和只有一项，那么a与b的关系是什么？
阅读下列材料．当抛物线的关系式中含有字母系数时，随着系数中的字母取值不同，抛物线的顶点坐标也将发生变化．
例如，由抛物线y＝x2－2mx＋m2＋2m－1①，有y＝(x－m)2＋2m－1②，
∴抛物线的顶点坐标为(m，2m－1)，即
当m的值变化时，x，y的值也随之变化，因而y值也随着x值的变化而变化，将③代入④，得y＝2x－1⑤．
可见，不论m取何实数，抛物线顶点的纵坐标y和横坐标x满足关系式y＝2x－1．解答下列问题：
(1)上述过程中，由①到②所用的数学方法是________，其中运用了________公式，由③，④到⑤所用的数学方法是________；
(2)根据阅读材料提供的方法，确定抛物线y＝x2－2mx＋2m2－3m＋1的顶点纵坐标y与横坐标x之间的关系式．
观察可得最简公分母是(x＋1)(x－1)，方程两边乘最简公分母，可以把分式方程转化为整式方程求解．
【解答】
（2）方程的两边同乘(x＋1)(x－1)，得
2(x－1)＋4＝x2－1，
即x2－2x－3＝0，
(x－3)(x＋1)＝0，
解得x1＝3，x2＝－1，
检验：把x＝3代入(x＋1)(x－1)＝8≠0，即x＝3是原分式方程的解，
把x＝－1代入(x＋1)(x－1)＝0，即x＝－1不是原分式方程的解，
则原方程的解为：x＝3．
【点评】此题考查了
实数的混合运算与分式方程的解法．此题难度不大，但注意掌握绝对值的性质、负指数幂的性质、零指数幂的性质以及特殊角的三角函数值，注意解分式方程一定要验根．
20．（本题满分5分）如图，已知△ABC，且∠ACB＝90°。
（1）请用直尺和圆规按要求作图（保留作图痕迹，不写作法和证明）；
①以点A为圆心，BC边的长为半径作⊙A；
②以点B为顶点，在AB边的下方作∠ABD=∠BAC．
（2）请判断直线BD与⊙A的位置关系（不必证明）．
 |
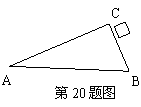由抛物线y＝x2－2mx＋m2＋2m－1，①有y＝(x－m)2＋2m－1，②
∴抛物线的顶点坐标为(m，2m－1)，即
当m的值变化时，x，y的值也随之变化，同时y的值也随x的值的变化而变化，将③代入④，得y＝2x－1．
可见，不论m取何实数，抛物线顶点的纵坐标y和横坐标x都满足关系式y＝2x－1．回答下列问题．
(1)上述过程中，由①到②所用的数学方法是________，其中运用了________公式，由③④到⑤所用的数学方法是________；
(2)根据阅读材料提供的方法，确定抛物线y＝x2－2mx＋2m2－3m＋1的顶点的纵坐标y与横坐标x之间的关系式．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com