
题目列表(包括答案和解析)
 观察图,回答问题.
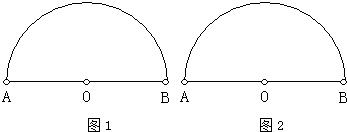
观察图,回答问题.如图(1)要将一块直径为2m的半圆形铁皮加工成一个圆柱的两个底面和一个圆锥的底面.

操作:
方案一:在图(1)中设计 一个使圆柱一个底面最大,半圆形铁皮得以充分利用的方案(要求:画示意图).
方案二:在图(2)中设计一个使圆柱两个底面最大,半圆形铁皮得以充分利用的方案(要求:画示意图).
探究:(1)求方案一中圆锥底面的半径.(2)求方案(2)中,圆 锥底面的半径.(3)设方案二中半圆圆心为O,圆柱两个底面的圆心为O1,O2,圆锥底面的圆心为O3,试判断以O1,O2,O3,O为顶点四边形是什么样的特殊四边形,并加以证明求解.
 25、问题:要将一块直径为2m的半圆形铁皮加工成一个圆柱的两个底面和一个圆锥的底面.
25、问题:要将一块直径为2m的半圆形铁皮加工成一个圆柱的两个底面和一个圆锥的底面.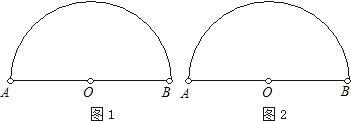
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com