题目列表(包括答案和解析)
因为cos30º＝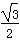
，cos210º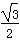＝－，所以cos210º＝cos(180º＋30º)＝－cos30º＝－；
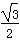因为cos45º＝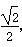
cos225º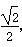＝－所以cos225º＝cos(180º＋45º)＝－cos45º＝－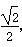
猜想：一般地，当
为锐角时，有cos(180º＋)＝－cos．由此可知cos240º＝ ．
，cos210º＝－，所以cos210º＝cos(180º＋30º)＝－cos30º＝－；
cos225º＝－所以cos225º＝cos(180º＋45º)＝－cos45º＝－
为锐角时，有cos(180º＋)＝－cos．由此可知cos240º＝ ．在研究三角形内角和等于180°的证明方法时，小明和小虎分别给出了下列证法．
小明：在△ABC中，延长BC到D，
∴∠ACD＝∠A＋∠B(三角形一个外角等于和它不相邻的两个内角的和)．
又∵∠ACD＋∠ACB＝180°(平角定义)，
∴∠A＋∠B＋∠ACB＝180°(等式的性质)．
小虎：在△ABC中，作CD⊥AB(如图)，
∵CD⊥AB(已知)，
∴∠ADC＝∠BDC＝90°(直角定义)．
∴∠A＋∠ACD＝90°，∠B＋∠BCD＝90°(直角三角形两锐角互余)．
∴∠A＋∠ACD＋∠B＋∠BCD＝180°(等式的性质)．
∴∠A＋∠B＋∠ACB＝180°．
请你判断上述两名同学的证法是否正确，如果不正确，写出一种你认为较简单的证明三角形内角和定理的方法，与同伴交流．
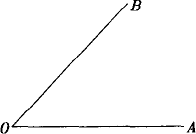
如图已知，锐角∠AOB，
求作∠β使得∠β＝180°－2∠AOB．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com