编一个方程，使它的解为x=-．

　　当总体中的个体数较多时，采用简单随机抽样显得较为费事．这时，可将总体分成均衡的几个部分，然后按照预先定出的规则，从每一部分抽取1个个体，得到所需要的样本，这种抽样叫做系统抽样．

　　例如，为了了解参加某种知识竞赛的1000名学生的成绩，打算从中抽取一个容量为50的样本．假定这1000名学生的编号是1，2，…，1000，由于50∶1000＝1∶20，我们将总体均分成50个部分，其中每一部分包括20个个体．例如第1部分的个体的编号是1，2，…，20．然后在第1部分随机抽取一个号码，比如它是第18号，那么可以从第18号起，每隔20个抽取1个号码，这样得到一个容量为50的样本：18，38，58，…，978，998．

　　上面，由于总体中的个体数1000正好能被样本容量50整除，可以用它们的比值作为进行系统抽样的间隔．如果不能整除，比如总体中的个体数为1003，样本容量仍为50，这时可用简单随机抽样先从总体中剔除3个个体(可利用随机数表)，使剩下的个体数1000能被样本容量50整除，然后再按系统抽样方法往下进行．因为总体中的每个个体被剔除的机会相等，也就是每个个体不被剔除的机会相等，所以在整个抽样过程中每个个体被抽取的机会仍然相等．

　　系统抽样的步骤可概括为：

　　(1)采用随机的方式将总体中的个体编号．为简便起见，有时可直接利用个体所带有的号码，如考生的准考证号、街道上各户的门牌号，等等．

　　(2)为将整个的编号分段(即分成几个部分)，要确定分段的间隔k．当(N为总体中的个体数，n为样本容量)是整数时，k＝；当不是整数时，通过从总体中剔除一些个体使剩下的总体中个体个数能被n整除，这时k＝．

　　(3)在第1段用简单随机抽样确定起始的个体编号l．

　　(4)按照事先确定的规则抽取样本．通常是将l加上间隔k，得到第2个编号l＋k，再将(l＋k)加上k，得到第3个编号l＋2k，这样继续下去，直到获取整个样本．

在10000个有机会中奖的号码(编号为0000～9999)中，有关部门按照随机抽取的方式确定后两位数字为37的号码为中奖号码．这是运用哪种抽样方法来确定中奖号码的？试依次写出这100个中奖号码的开始3个和最后3个．

    课题研究：现有边长为120厘米的正方形铁皮，准备将它设计并制成一个开口的水槽，使水槽能通过的水的流量最大．初三（1）班数学兴趣小组经讨论得出结论：在水流速度一定的情况下，水槽的横截面面积越大，则通过水槽的水的流量越大．为此，他们对水槽的横截面进行了如下探索：

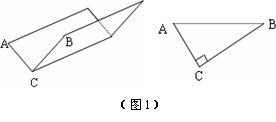
⑴方案①：把它折成横截面为直角三角形的水槽（如图1）．

若∠ACB=90°，设AC=x厘米，该水槽的横截面面积为y厘米²，请你写出y关于x的函数关系式（不必写出x的取值范围），并求出当x取何值时，y的值最大，最大值又是多少？

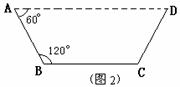
方案②：把它折成横截面为等腰梯形的水槽（如图2）．

若∠ABC=120°，请你求出该水槽的横截面面积的最大值，并与方案①中的y的最大值比较大小．

⑵假如你是该兴趣小组中的成员，请你再提供两种方案，使你所设计的水槽的横截面面积更大．画出你设计的草图，标上必要的数据（不要求写出解答过程）．（习题改编）