
题目列表(包括答案和解析)
设△ABC的3条边长分别是a、b、c,且 ,
,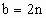 ,
,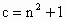 .
.
(1)填表:
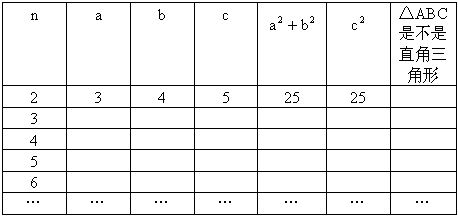
(2)当n取大于1的整数时,以表中各组a、b、c的值为边长构成的三角形都是直角三角形吗?为什么?
(3)3、4、5是一组勾股数,把这3个数分别扩大2倍,所得的3个数还是勾股数吗?扩大3倍、4倍和k倍呢?为什么?
(4)还有不同于上述各组数的勾股数吗?若有,请举例.
 6、观察下列图形并填表: 6、观察下列图形并填表:
|
我们知道两条直线相交,一共有两对对顶角、4对邻补角,那么三条直线、四条直线,甚至是几条直线交于一点或两两相交有多少对对顶角和邻补角?请动手操作,观察填表,并归纳。

 ……
……
① ② ③
(1)请观察上图并填写下表:
| 图形编号 | ① | ② | ③ | …… |
| 对顶角的对数 | 2 | 6 | 12 | |
| 邻补角的对数 | 4 | 12 | 24 | |
 于点A、B,交抛物线C2:
于点A、B,交抛物线C2: 于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.
于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.| m | 1 | 2 | 3 |
 | | | |
 = .请证明你的猜想.
= .请证明你的猜想.
如图①,在平面直角坐标系中,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1: 于点A、B,交抛物线C2:
于点A、B,交抛物线C2: 于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.
于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.
【猜想与证明】
填表:
|
m |
1 |
2 |
3 |
|
|
|
|
|
由上表猜想:对任意m(m>0)均有 =
.请证明你的猜想.
=
.请证明你的猜想.
【探究与应用】
(1)利用上面的结论,可得△AOB与△CQD面积比为 ;
(2)当△AOB和△CQD中有一个是等腰直角三角形时,求△CQD与△AOB面积之差;
【联想与拓展】
如图②过点A作y轴的平行线交抛物线C2于点E,过点D作y轴的平行线交抛物线C1于点F.在y轴上任取一点M,连接MA、ME、MD和MF,则△MAE与△MDF面积的比值为 .

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com