
题目列表(包括答案和解析)
丰富的图形世界里有奇妙的数量关系,让我们通过下面这些几何体开始神奇的探索之旅.
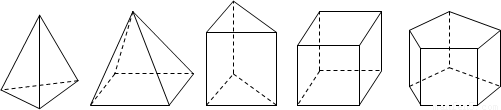
观察:下面这些几何体都是简单几何体,请您仔细观察.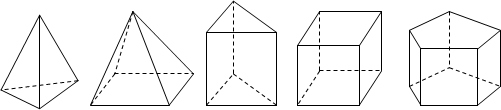
统计:每个几何体都会有棱(棱数为E)、面(面数为F)、顶点(顶点数为V),现将有关数据统计,完成下表.
| 几何体 | a | b | c | d | e |
| 棱数(E) | 6 | | 9 | | 15 |
| 面数(F) | 4 | 5 | 5 | 6 | |
| 顶点数(V) | 4 | 5 | | 8 | |
 ;
;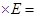 3
3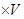 .
.丰富的图形世界里有奇妙的数量关系,让我们通过下面这些几何体开始神奇的探索之旅.
观察:下面这些几何体都是简单几何体,请您仔细观察.
统计:每个几何体都会有棱(棱数为E)、面(面数为F)、顶点(顶点数为V),现将有关数据统计,完成下表.
|
几何体 |
a |
b |
c |
d |
e |
|
棱数(E) |
6 |
|
9 |
|
15 |
|
面数(F) |
4 |
5 |
5 |
6 |
|
|
顶点数(V) |
4 |
5 |
|
8 |
|
发现:(1)简单几何中,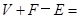 ;
;
(2)简单几何中,每条棱都是 个面的公共边;
(3)在正方体中,每个顶点处有 条棱,每条棱都有 个顶点,所以有2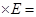 3
3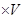 .
.
应用:有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.请问它有 条棱, 个顶点,每个顶点处有 条棱.
丰富的图形世界里有奇妙的数量关系,让我们通过下面这些几何体开始神奇的探索之旅.
观察:下面这些几何体都是简单几何体,请您仔细观察.
统计:每个几何体都会有棱(棱数为E)、面(面数为F)、顶点(顶点数为V),现将有关数据统计,完成下表.
| 几何体 | a | b | c | d | e |
| 棱数(E) | 6 | 9 | 15 | ||
| 面数(F) | 4 | 5 | 5 | 6 | |
| 顶点数(V) | 4 | 5 | 8 |
发现:(1)简单几何中,![]() ;
;
(2)简单几何中,每条棱都是 个面的公共边;
(3)在正方体中,每个顶点处有 条棱,每条棱都有 个顶点![]() ,
,
所以有2![]() 3
3![]() .
.
应用: 有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它 的每个顶点处都有相同数目的棱.
请问它有 条棱, 个顶点,每个顶点处有 条棱.
丰富的图形世界里有奇妙的数量关系,让我们通过下面这些几何体开始神奇的探索之旅.
观察:下面这些几何体都是简单几何体,请你仔细观察.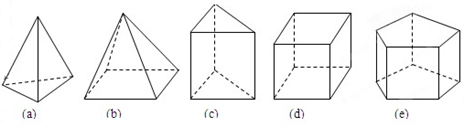
统计:每个几何体都会有棱(棱数为E)、面(面数为F)、顶点(顶点数为V),现将有关数据统计,完成下表.
| 几何体 | a | b | c | d | e |
| 棱数(E) | 6 | 9 | 15 | ||
| 面数(F) | 4 | 5 | 5 | 6 | |
| 顶点数(V) | 4 | 5 | 8 |
发现:(1)简单几何中,V+F-E=______;
(2)简单几何中,每条棱都是______个面的公共边;
(3)在正方体中,每个顶点处有______条棱,每条棱都有______个顶点,所以有2×E=3×V.
应用:有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.请问它有______条棱,______个顶点,每个顶点处有______条棱.

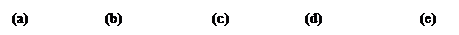
| 几何体 | a | b | c | d | e |
| 棱数(E) | 6 | | 9 | | 15 |
| 面数(F) | 4 | 5 | 5 | 6 | |
| 顶点数(V) | 4 | 5 | | 8 | |
 ;
; 3
3 .
.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com