
题目列表(包括答案和解析)
(本题12分) 在正方形网格中以点 为圆心,
为圆心,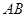 为半径作圆
为半径作圆 交网格于点
交网格于点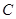 (如图(1)),过点
(如图(1)),过点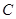 作圆的切线交网格于点
作圆的切线交网格于点 ,以点
,以点 为圆心,
为圆心, 为半径作圆交网格于点
为半径作圆交网格于点
(如图(2)).
![]() 问题:
问题:
(1)求![]() 的度数;
的度数;
(2)求证: ![]() ;
;
(3)![]() 可以看作是由
可以看作是由![]() 经过怎样的变换得到的?并判断
经过怎样的变换得到的?并判断![]() 的形状(不用说明理由).
的形状(不用说明理由).
(4)如图(3),已知直线 ,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形
,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形 ,使三个顶点
,使三个顶点 ,分别在直线
,分别在直线 上.要求写出简要的画图过程,不需要说明理由.
上.要求写出简要的画图过程,不需要说明理由.
(本题12分) 在正方形网格中以点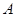 为圆心,
为圆心,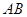 为半径作圆
为半径作圆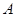 交网格于点
交网格于点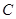 (如图(1)),过点
(如图(1)),过点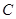 作圆的切线交网格于点
作圆的切线交网格于点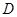 ,以点
,以点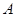 为圆心,
为圆心,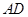 为半径作圆交网格于点
为半径作圆交网格于点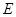
(如图(2)).
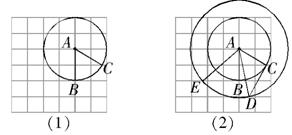
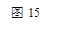 问题:
问题:
(1)求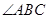 的度数;
的度数;
(2)求证: 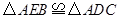 ;
;
(3)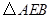 可以看作是由
可以看作是由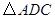 经过怎样的变换得到的?并判断
经过怎样的变换得到的?并判断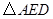 的形状(不用说明理由).
的形状(不用说明理由).
(4)如图(3),已知直线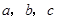 ,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形
,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形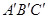 ,使三个顶点
,使三个顶点 ,分别在直线
,分别在直线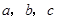 上.要求写出简要的画图过程,不需要说明理由.
上.要求写出简要的画图过程,不需要说明理由.

(本题12分) 如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其顶点为
,其顶点为![]() ,且直线
,且直线![]() 的解析式为
的解析式为![]() .
.
1.(1) 求二次函数的解析式.
2.(2) 求△ABC外接圆的半径及外心的坐标;
3.(3) 若点P是第一象限内抛物线上一动点,求四边形ACPB的面积最大值.

(本题12分)如图①,平面直角坐标系中,已知C(0,10),点P、Q同时从点出发,在线段OC上做往返匀速运动,设运动时间为t(s),点P、Q离开点O的距离为S图②中线段OA、OB(A、B都在格点上)分别表示当0≤t≤6时P、Q两点离开点O的距离S与运动时间t (s)的函数图像.
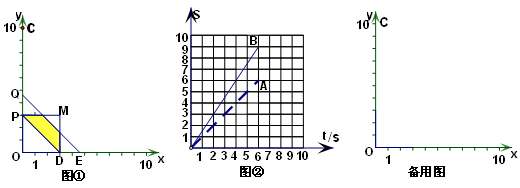
1.⑴请在图②中分别画出当6≤t≤10时P、Q两点离开点O的距离S与运动时间t(s)的函数图像.
2.⑵求出P、Q两点第一次相遇的时刻.
3.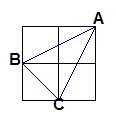
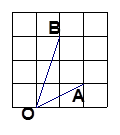 ⑶如图①,在运动过程中,以OP为一边画正方形OPMD,点D在x轴正半轴上,作QE∥PD交x轴于E,设△PMD与△OQE重合部分的面积 为y,试求出当0≤t≤10时y与t(s)的函数关系式(写出相应的t的范围) .
⑶如图①,在运动过程中,以OP为一边画正方形OPMD,点D在x轴正半轴上,作QE∥PD交x轴于E,设△PMD与△OQE重合部分的面积 为y,试求出当0≤t≤10时y与t(s)的函数关系式(写出相应的t的范围) .
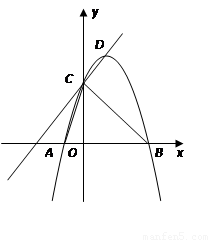
(本题12分) 如图,已知二次函数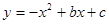 的图象与
的图象与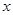 轴交于点
轴交于点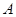 、
、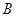 ,与
,与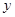 轴交于点
轴交于点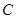 ,其顶点为
,其顶点为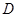 ,且直线
,且直线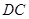 的解析式为
的解析式为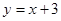 .
.
1.(1) 求二次函数的解析式.
2.(2) 求△ABC外接圆的半径及外心的坐标;
3.(3) 若点P是第一象限内抛物线上一动点,求四边形ACPB的面积最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com