
题目列表(包括答案和解析)
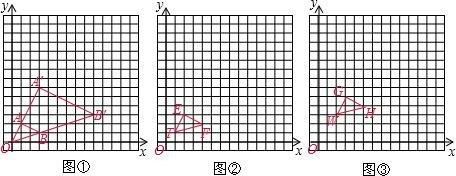
| 表格 | 表一 | 表二 | 表三 | |||
| 位似中心 | O(0,0) | T(1,1) | W(2,3) | |||
| 比例尺 | 3:1 | 3:1 | 4:1 | |||
| 点的坐标 | A(1,2) | B(3,1) | E(2,3) | F(4,2) | G(3,5) | H(5,4) |
| 对应点坐标 | A′(3,6) | B(9,3) | E′( ) | F′( ) | G′( ) | H′( ) |
| 猜想结论 | 点P(x,y)的对应点P′的坐标为(3x,3y) | 点P(x,y)的对应点P′的坐标为( ) | 点Q(x,y)的对应点Q′的坐标为( ) | |||
在“我与中国队同登珠峰”活动中,为模拟测量营地边冰塔林中的冰柱的高度,某小组的同学设计了如下方案:
方案一:根据光的反射定律,利用一面镜子和一根皮尺,进行测量.
把镜子放在离冰柱(AB)8.7米的点E处,然后沿着直线BE后退到D,这时恰好在镜子里看到冰柱顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.6米,请你计算冰柱(AB的高度(精确到0.1米).
如果提供测量的工具有①皮尺一根;②教学用三角板一副;③长为2.5米的标杆一根;④高度为1.5米的测角仪(能测量仰角、俯角的仪器)一架.
请你也设计一个方案并回答下列问题:
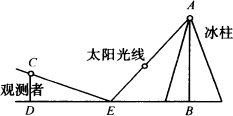
(1)在下图画出你的测量方案示意图;
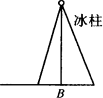
(2)你需要测得示意图中哪些数据,并分别用a、b、c、d等表示测得的数据________.
(3)写出求冰柱高的算式:AB=________.
调查班里同学的人际关系.
一、设计 调查问卷
问卷编号:________年________月________日
调查目的 了解班里同学的人际关系
调查对象 性别 年龄 职业
调查内容
(1)你能背出几个本班同学家的电话号码吗? ( )
A.多于7个 B.4~7个 C.0~3个
(2)你在本班的朋友多,还是外班的朋友多? ( )
A.本班的多 B.一样多 C.外班的多
(3)在班里,你是“小领袖”,还是“小随从”? ( )
A.我没考虑过 B.大多数人听我的话 C.多数情况下我听别人的
(4)你觉得可不可以向老师打小报告? ( )
A.不行 B.最好不要 C.当然可以
(5)如果朋友搞你的恶作剧,你会怎么样? ( )
A.和他们一起笑
B.看自己心情如何,也许和他们一起大笑,也许生气发怒
C.生气发怒
(6)当你的同学有困难时,他们是否愿意求得你的帮助? ( )
A.非常愿意 B.只有关系密切的同学才来求助 C.不愿意
(7)当朋友向你吐露了一个极有趣的个人问题后,你会怎么样? ( )
A.没有考虑是否要把这件事报告别人
B.努力保守秘密
C.在朋友离开后不久,便找个第三者参与评论
二、实施调查
三、处理数据
以选择A得3分、B、得2分、C得0分计算整理.21~15分的人在班里受大家欢迎,和大家相处很好;15~5分的人有自己的朋友圈子,但很少关心圈外的人;4~0分的人在班里朋友很少.
四、交流
发现班里同学人际关系好的要多关心帮助那些孤独的人,并提醒那些在班里朋友很少的人要多关心他人,不要只想着自己,要多参加集体活动.
五、写一份调查报告.
表 长江足球队成绩
年份场次 1997 1998 1999 2000 2001 2002
第一场 +3 +2 -2 -1 +4 0
第二场 +1 -3 +3 -4 0 -1
合计

其中用-x表示净输x个球.用+x表示净赢x个球。用0表示平局。
请您帮忙计算一下以上六年合计分别是多少?
1997年:__________ 1998年:__________
1999年:__________ 2000年:__________
2001年:__________ 2002年:__________
六年净胜球总计:_________.
思考:以上结果你是如何得出的?
(1)同号两数如何相加?(2)异号两数如何相加?(3)一个数与零相加和是多少?
观察是思考的“外壳”,要想思考得好,一定要善于观察.数学家在发现或解决问题时往往首先依赖于他对若干现象的观察--通过观察,如果发现某种值得注意的规律,就对它进行研究,并力图从中发现某种结论,去解释或描述这种模型,以求问题的顺利解决.例如,如果让你用任意方法去切一块圆饼,只要通过同一点不超过两刀,那么最多能得到几块?
自然,我们用不着特地去买一块饼来,只要在纸上画一些圆就行了.我们对各圆进行不同次数的切割,并在表中记录结果,得到:

我们仔细考查一下这张表,看看能否找到其中的规律.从记录上看,增加的块数分别是自然数1,2,3.切割次数也分别是1,2,3.这种规律是否继续有效呢?让我们再多试几次,并记录数据,得到:

现在的增加数分别是1,2,3,4,5,可见规律继续有效.这种规律使我们预测到:切割6次得22块,切割7次得29块.并进一步能使我们预测切割任意次所得的块数.
想一想:切割8次、9次将分别得到多少块?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com