
题目列表(包括答案和解析)
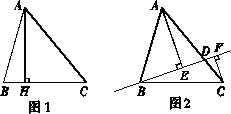
如图1和图2,在△ABC中,AB=13,BC=14,cos∠ABC=![]() .
.
探究
在如图1,AH⊥BC于点H,则AH=________,AC=________,△ABC的面积S△ABC=________.
拓展
如图2,点D在AC上(可与点A,B重合),分别过点A,C作直线BD的垂线,垂足为E,F.设BD=x,AE=m,CF=n.(当点D与点A重合时,我们认为S△ABC=0.
(1)用含x,m或n的代数式表示S△ABD及S△CBD;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值.
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现
请你确定一条直线,使得A,B,C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.
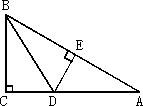
某同学探究画直角三角形中锐角的平分线,方法如下:如图,在斜边AB上取一点E,使BE=BC,过点E作DE⊥AB,与AC交于点D,则BD为∠ABC的平分线,这种画法正确吗?并说明理由.
探究问题
(1)阅读理解:
①如图1,在△ABC所在平面上存在一点P,使它到三角形三顶点的距离之和最小,则称点P为△ABC的费马点,此时PA+PB+PC的值为△ABC的费马距离.
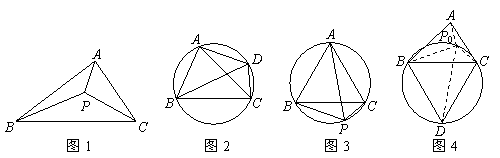 ②如图2,若四边形ABCD的四个顶点在同一个圆上,则有AB·CD+BC·AD=AC·BD.此为托勒密定理.
②如图2,若四边形ABCD的四个顶点在同一个圆上,则有AB·CD+BC·AD=AC·BD.此为托勒密定理.
(2)知识迁移:
①请你利用托勒密定理,解决如下问题:
如图3,已知点P为等边△ABC外接圆的弧BC上任意一点.求证:PB+PC=PA.
②根据(2)①的结论,我们有如下探寻△ABC(其中∠A、∠B、∠C均小于120º)的费马点和费马距离的方法:
第一步:如图4,在△ABC的外部以BC为边长作等边△BCD及其外接圆;
第二步:在弧BC上取一点P0,连接P0A、P0B、P0C、P0D.
易知P0A+P0B+P0C=P0A+(P0B+P0C)=P0A+ ;
第三步:请你根据(1)①中定义,在图4中找出△ABC的费马点P,线段 的长度即为△ABC的费马距离.
(3)知识应用:
2010年4月,我国西南地区出现了罕见的持续干旱现象,许多村庄出现了人、畜饮水困难.为解决老百姓饮水问题,解放军某部到云南某地打井取水.
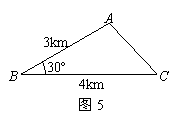 已知三村庄A、B、C构成了如图5所示的△ABC(其中∠A、∠B、∠C均小于120º),现选取一点P打水井,使水井P到三村庄A、B、C所铺设的输水管总长度最小.求输水管总长度的最小值.
已知三村庄A、B、C构成了如图5所示的△ABC(其中∠A、∠B、∠C均小于120º),现选取一点P打水井,使水井P到三村庄A、B、C所铺设的输水管总长度最小.求输水管总长度的最小值.
如图,在四边形A8CD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).
(温馨提示:在图中,连结BD,取BD的中点H,连结HE、HF,根据三角形中位线定理,可证得HE=HF,从而∠HFE=∠HEF,再利用平行线的性质,可证得∠BME=∠CNE.)

问题一:如图,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连结EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论.
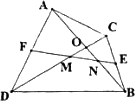
问题二:如图,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G,若∠EFC=600,连结GD,判断△AGD的形状并证明.

已知,在等腰△ABC中,AB=AC,在射线CA上截取线段CE,在射线AB上截取线段BD,连结DE,DE所在直线交直线BC于点M.
请探究:
(1) 如图①,当点E在线段AC上,点D在AB延长线上时,若BD=CE,
请判断线段MD和线段ME的数量关系,并证明你的结论;
(2) 如图②,当点E在CA的延长线上,点D在AB的延长线上时,若BD=CE,
则(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由。
(3)如图③,当点E在CA的延长线上,点D在线段AB上(点D不与A、B重合),DE所在直线与直线BC交于点M,若CE=mBD,(m>1),请你判断线段MD与线段ME的数量关系,并说明理由。
  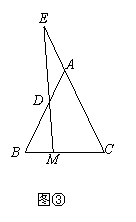 | |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com