
题目列表(包括答案和解析)
读理解下列例题,再完成练习.
例题:解不等式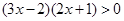
解:由有理数的乘法方法可知“两数相乘,同号得正”,因此可得
①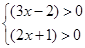 ②
②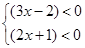
解不等式组①得 解不等式组②得
解不等式组②得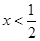
所以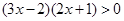 的解集
的解集 或
或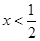 (2)
(2)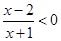
读理解下列例题,再完成练习.
例题:解不等式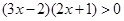
解:由有理数的乘法方法可知“两数相乘,同号得正”,因此可得
①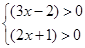 ②
②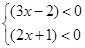
解不等式组①得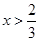 解不等式组②得
解不等式组②得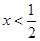
所以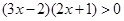 的解集
的解集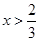 或
或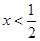 (2)
(2)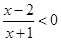

 ②
②
 解不等式组②得
解不等式组②得
 的解集
的解集 或
或 (2)
(2)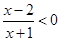
先阅读理解下列例题,再完成作业:
例题:解不等式(3x-2)(2x+1)>0.
解:由有理数的乘法方法知道“两数相乘,同号得正”,因此可得①![]() 或②
或②![]()
解不等式组①得x>![]() ,解不等式组②得x<-
,解不等式组②得x<-![]()
所以(3x-2)(2x+1)>0的解集应是x>![]() 或x<-
或x<-![]() .
.
作业:(1)求不等式![]() <0的解集;
<0的解集;
(2)通过阅读例题和做作业(1),你学会了什么知识和方法?
先阅读理解下列例题,再完成作业:
例题:解不等式(3x-2)(2x+1)>0.
解:由有理数的乘法方法知道“两数相乘,同号得正”,因此可得①![]() 或②
或②![]()
解不等式组①得x>![]() ,解不等式组②得x<-
,解不等式组②得x<-![]()
所以(3x-2)(2x+1)>0的解集应是x>![]() 或x<-
或x<-![]()
作业:(1)求不等式![]() <0的解集.
<0的解集.
(2)通过阅读例题和做作业(1),你学会了什么知识和方法?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com