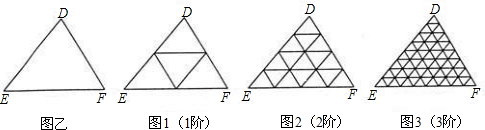
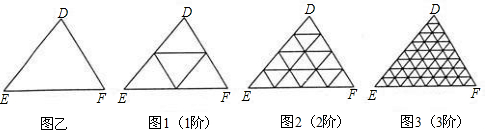
如图,将一个三角形的三边依次都分成2、3、4……等分,并将分点按图1、图2、图3那样连起来,这样,每个图中所得到的小三角形都会全等.按此方法,当三边都分成10等分时,所得到的全等小三角形的个数是(    ).

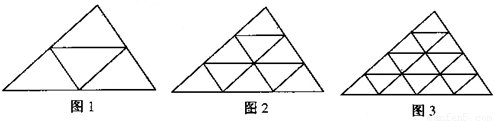
A . 98           B . 99             C . 100         D. 101

一般地，“任意三角形都是自相似图形”，只要顺次连接三角形各边中点，则可将原三角形分割为四个都与它自己相似的小三角形．我们把△DEF（图乙）第一次顺次连接各边中点所进行的分割，称为1阶分割（如图1）；把1阶分割得出的4个三角形再分别顺次连接它的各边中点所进行的分割，称为2阶分割（如图2）…，依此规则操作下去．n阶分割后得到的每一个小三角形都是全等三角形（n为正整数），设此时小三角形的面积为S_n．请写出一个反映S_n-1，S_n，S_n+1（n＞1）之间关系的等式________．

(1)由二十边形的一个顶点能画出多少条对角线？

(观察教村第54页图8.3.4，这一问题一定很容易解决，right？)

(2)四边形，五边形，…，n边形，各有多少条对角线？

(这一问题不大好解决．请与同伴讨论，试试看，相信你能行！)

(3)对角线如不相交，在五边形、六边形、七边形内分别最多能画出几条对角线？

(4)图中的多边形ABCDEF，可以用3条对角线AC、AD与DF分成三角形．试找出其他两种用3条对角线将它分割成三角形的不同方法．

(5)图中的七边形则是被4条对角线分割成三角形．你还能找出多少种其他的方法？

有一种方法可以很清楚地记录不同的分割方法，那就是依次计算各顶点处的三角形数目．上图的分割方法可以记录为：

1　　4　　1　　3　　1　　3　　2

它们的和(不论自哪个顶点开始，不论是顺时针或逆时针方向，都会得到相同的数字)：

1＋4＋1＋3＋1＋3＋2＝15．

以不同方式分割七边形是否会得到相同的数字？它们的和呢？

请解释你的结果．

取不同边数的多边形，并记录不同的分割方法；然后试试自己是否不用绘图就预测出十边形会有多少种不同的分割方法．