
题目列表(包括答案和解析)
如图11所示,在梯形ABCD中,已知AB∥CD, AD⊥DB,AD=DC=CB,AB=4.以AB所在直线为![]() 轴,过D且垂直于AB的直线为
轴,过D且垂直于AB的直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求∠DAB的度数及A、D、C三点的坐标;
(2)求过A、D、C三点的抛物线的解析式及其对称轴L.
(3)若P是抛物线的对称轴L上的点,那么使![]() PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)
PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)
 方案设计:儿童公园有一块半圆形空地,如图11所示,根据需要欲在此半圆内划出一个三角形区域作为健身场地,其中内接于此三角形的矩形区域为儿童游乐场,已知半圆的直径AB=100米,若使三角形的顶点C在半圆上,且AC=80米.
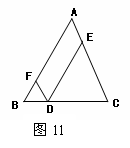
方案设计:儿童公园有一块半圆形空地,如图11所示,根据需要欲在此半圆内划出一个三角形区域作为健身场地,其中内接于此三角形的矩形区域为儿童游乐场,已知半圆的直径AB=100米,若使三角形的顶点C在半圆上,且AC=80米.如图11所示,已知D是等腰三角形ABC底边BC上的一点,点E,F分别在AC,AB上,且DE∥AB,DF∥AC
求证:DE+DF=AB
 |
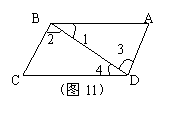
如图11所示,下列推理中正确的数目有( )
①因为∠1=∠4,所以BC∥AD.②因为∠2=∠3,所以AB∥CD.
③因为∠BCD+∠ADC=180°,所以AD∥BC.④因为∠1+∠2+∠C=180°,所以BC∥AD.
 |
(A)1个 (B)2个 (C)3个 (D)4个
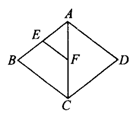
如图11所示,在菱形ABCD中,E、F分别是AB、AC的中点,如果EF=2,那么ABCD的周长是( )
A.4 B.8 C.12 D.16
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com