
题目列表(包括答案和解析)
某课题小组对课本的习题进行了如下探索,请逐步思考并解答
1.(人教版教材习题24.4的第2题)如图1,两个大小一样的传送轮连接着一条传送带,两个传动轮中心的距离是10m,求这条传送带的长_________.[

2.如图2、将传动轮增加到3个,每个传动轮的直径是3m,每两个传动轮中心的距离是10m, 求这条传送带的长__________.

3.改变动态关系,将静态问题升华为动态问题:
如图3,一个半径为1cm的⊙P沿边长为2πcm的等边三角形△ABC的外沿作无滑动滚动一周,求圆心P经过的路径长?⊙P自转了多少周?
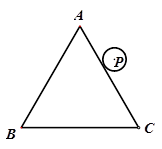
4.拓展与应用
如图4,一个半径为1cm的⊙P沿半径为3cm的⊙O外沿作无滑动滚动一周,则⊙P自转了多少周?

某课题小组对课本的习题进行了如下探索,请逐步思考并解答
1.(人教版教材习题24.4的第2题)如图1,两个大小一样的传送轮连接着一条传送带,两个传动轮中心的距离是10m,求这条传送带的长_________.[

2.如图2、将传动轮增加到3个,每个传动轮的直径是3m,每两个传动轮中心的距离是10m, 求这条传送带的长 __________.

3.改变动态关系,将静态问题升华为动态问题:
如图3,一个半径为1cm的⊙P沿边长为2πcm的等边三角形△ABC的外沿作无滑动滚动一周,求圆心P经过的路径长?⊙P自转了多少周?

4.拓展与应用
如图4,一个半径为1cm的⊙P沿半径为3cm的⊙O外沿作无滑动滚动一周,则⊙P自转了多少周?

四边形ABCD中,点E是AB的中点,F是AD边上的动点.连结DE、CF.
(1)若四边形ABCD是矩形,AD=12,CD=10,如图(1)所示.

①请直接写出AE的长度;
②当DE⊥CF时,试求出CF长度.
(2)如图(2),若四边形ABCD是平行四边形,DE与CF相交于点P.
探究:当∠B与∠PC满足什么关系时,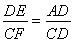 成立?并证明你的结论.
成立?并证明你的结论.

四边形ABCD中,点E是AB的中点,F是AD边上的动点.连结DE、CF.
(1)若四边形ABCD是矩形,AD=12,CD=10,如图(1)所示.
①请直接写出AE的长度;
②当DE⊥CF时,试求出CF长度.
(2)如图(2),若四边形ABCD是平行四边形,DE与CF相交于点P.
探究:当∠B与∠PC满足什么关系时, 成立?并证明你的结论.
成立?并证明你的结论.
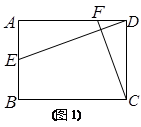
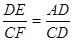 成立?并证明你的结论.
成立?并证明你的结论.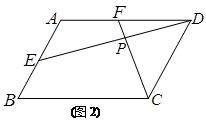
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com