
题目列表(包括答案和解析)
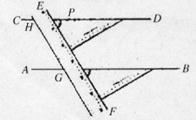 10、我们可以用直尺和三角尺画平行线,如图,在这一过程中,所用到的判断两直线平行的方法是
10、我们可以用直尺和三角尺画平行线,如图,在这一过程中,所用到的判断两直线平行的方法是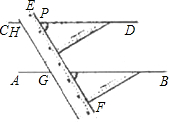 我们可以用直尺和三角尺画平行线,如图,在这一过程中,所用到的判断两直线平行的方法是________.
我们可以用直尺和三角尺画平行线,如图,在这一过程中,所用到的判断两直线平行的方法是________.
| |||||
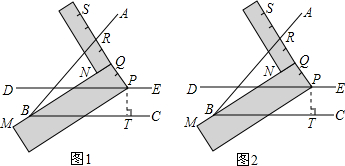 (1)阅读理解:
(1)阅读理解: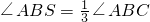 是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出
是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出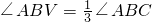 (无需写画法,保留画图痕迹即可).
(无需写画法,保留画图痕迹即可).湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com