
题目列表(包括答案和解析)
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC.点P从C点出发,沿线段CO以5个单位/秒的速度向终点O匀速运动,过点P作PH⊥OB,垂足为H.

(1)求点B的坐标;
(2)设△HBP的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;当t为何值时,△HBP的面积最大,并求出最大面积;
(3)分别以P、H为圆心,PC、HB为半径作⊙P和⊙H,当两圆外切时,求此时t的值.
【解析】(1)根据已知得出OB=OC=10,BN=OA=8,即可得出B点的坐标;
(2)利用△BON∽△POH,得出对应线段成比例,即可得出S与t之间的函数关系式;从而求出△HBP的最大面积;
(3)若⊙P和⊙H两圆外切 ,则须HB+PC=HP,从而求解
如图
1,在Rt△ABC中,∠C=90°,∠A=30°,∠B=60°.若BC=1,则根据“在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半”以及勾股定理容易得到AB=________,AC=________.因此,含30°角的直角三角形三边(从小到大)之比为________;同样,如图2,含45°角的直角三角形三边(从小到大)之比为________.这样结合三角函数的定义可以推导得到30°、45°、60°角的三角函数值.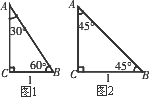
如图,若∠1+∠2+∠3+∠4=180°,可得直线________和________平行,根据是________;若使AB∥CD,则需要有________条件成立.

如图,在△ABC和△DEF中,∠A=∠D,AC=DF,若添加条件________=________或________∥________,可根据角边角条件说明△ABC≌△DEF;若添加条件________=________或________∥________,则可根据角角边条件得到△ABC≌△DEF;若添加条件________=________,则可根据边角边条件,得到△ABC≌△DEF
阅读理解:对于任意正实数a、b,∵ ≥0,∴
≥0,∴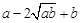 ≥0,
≥0,
∴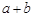 ≥
≥ ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在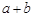 ≥
≥ (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥ ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值 .
.
(1)根据上述内容,回答下列问题:现要制作一个长方形(或正方形),使镜框四周围成的面积为4,请设计出一种方案,使镜框的周长最小。
设镜框的一边长为m(m>0),另一边的为 ,考虑何时时周长
,考虑何时时周长 最小。
最小。
∵m>0,  (定值),由以上结论可得:
(定值),由以上结论可得:
只有当m= 时,镜框周长 有最小值是 ;
有最小值是 ;
(2)探索应用:如图,已知A(-3,0),B(0,-4),P为双曲线 (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com