练习册

  • 练习册
  • 试题
    解方程:.22解方程: 【查看更多】

     

    题目列表(包括答案和解析)

    列方程解应用题
    （1）甲、乙两车同时从A城去B城，甲车每小时行35千米，乙车每小时行40千米，结果乙比甲提前半小时到达B城．问A、B两城间的路程有多少千米？
    （2）在2006年元月的日历上任意圈出一个竖列上相邻的3个数，请你根据这三个数的关系解决下列问题：
    若圈出的这三个数的和为51，则这三天分别是元月的多少号？它们都在星期几？
    日  一  二  三  四  五 六
     1   2   3   4   5   6   7
     8   9  10  11  12  13  14
    15  16  17  18  19  20  21
    22  23  24  25  26  27  28
    29  30  31        

    查看答案和解析>>

    列方程解应用题
    （1）甲、乙两车同时从A城去B城，甲车每小时行35千米，乙车每小时行40千米，结果乙比甲提前半小时到达B城．问A、B两城间的路程有多少千米？
    （2）在2006年元月的日历上任意圈出一个竖列上相邻的3个数，请你根据这三个数的关系解决下列问题：
    若圈出的这三个数的和为51，则这三天分别是元月的多少号？它们都在星期几？
    日  一  二  三  四  五 六
     1   2   3   4   5   6   7
     8   9  10  11  12  13  14
    15  16  17  18  19  20  21
    22  23  24  25  26  27  28
    29  30  31        

    查看答案和解析>>

    列方程（组）解应用题：
    某货主准备租用汽车运输公司的甲、乙两种货车将一批货物运往外地，为简便起见，假设该公司每辆货车每次出车都按标准载重量装满．该货主恰好看到这两种货车过去两次租用情况的表格如下：
    第一次 第二次
    甲种货车的数量（单位：辆） 2 5
    乙种货车的数量（单位：辆） 3 6
    累积运货的数量（单位：吨） y2 38
    （y）请d帮他计算一下每辆甲种货车每次能运多少吨货物？每辆乙种货车呢？
    （2）如果他有22吨货物需要运走，不考虑其它因素，那么他有几种租车方案？

    查看答案和解析>>

    解下列方程，将得到的解填入下面的表格中，观察表格中两个解的和与积，它们和原来的方程的系数有什么联系？
    （1）x2-2x=0（2）x2+3x-4=0（3）x2-5x+6=0
    方  程 x1 x2 x1+x2 x1．x2
    （1）
    0
    0
    2
    2
    2
    2
    0
    0
    （2）
    -4
    -4
    1
    1
    -3
    -3
    -4
    -4
    （3）
    2
    2
    3
    3
    5
    5
    6
    6
    请同学们仔细观察方程的解，你会发现方程的解与方程中未知数的系数和常数项之间有一定的关系．
    一般的，对于关于x的方程x2+px+q=0（p，q为常数，p2-4q≥0）的两根为x1、x2
    则x1+x2=
    -p
    -p
    ，x1．x2=
    q
    q
    ．
    （2）运用以上发现，解决下面的问题：
    ①已知一元二次方程x2-2x-7=0的两个根为x1，x2，则x1+x2的值为
    B
    B

    A．-2     B．2     C．-7     D．7
    ②已知x1，x2是方程x2-x-3=0的两根，利用上述结论，不解方程，求x12+x22的值．

    查看答案和解析>>

    在数学学习过程中，通常是利用已有的知识与经验，通过对研究对象进行观察、实验、推理、抽象概括，发现数学规律，揭示研究对象的本质特征．
    比如“同底数幂的乘法法则”的学习过程是利用有理数的乘方概念和乘法结合律，由“特殊”到“一般”进行抽象概括的：
    22×23=25，23×24=27，22×26=28，…?2m×2n=2m+n，…?am×an=am+n（m、n都是正整数）．我们亦知：
    2
    3
    ＜
    2+1
    3+1
    ，
    2
    3
    ＜
    2+2
    3+2
    ，
    2
    3
    ＜
    2+3
    3+3
    ，
    2
    3
    ＜
    2+4
    3+4
    ，…
    （1）请你根据上面的材料归纳出a、b、c（a＞b＞0，c＞0）之间的一个数学关系式；
    （2）试用（1）中你归纳的数学关系式，解释下面生活中的一个现象：“若m克糖水里含有n克糖，再加入k克糖（仍不饱和），则糖水更甜了”；
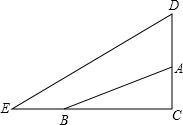    （3）如图，在Rt△ABC中，∠C=90°，CB=a，CA=b，AD=BE=c（a＞b），能否根据这个图形提炼出与（1）中相精英家教网同的关系式并给予证明．

    查看答案和解析>>


    同步练习册答案