如图，已知AB∥CD，∠AEC=90°，那么∠A与∠C的度数和为多少度？为什么？
解：∠A与∠C的度数和为　_________　．
理由：过点E作EF∥AB，
∵EF∥AB，
∴∠A+∠AEF=180°（　_________　）．
∵AB∥CD（　_________　），EF∥AB，
∴EF∥CD（　_________　）
∴　_________　（两直线平行，同旁内角互补）
∴∠A+∠AEF+∠CEF+∠C=　_________　°（等式的性质）
即∠A+∠AEC+∠C=　_________　°
∵∠AEC=90°（已知）
∴∠A+∠C=　_________　°（等式的性质）．

下列命题是真命题的是                                              （ 　）

　　(A)相等的角是对顶角　　              (B)两直线被第三条直线所截，内错角相等

　　(C)若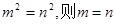　             (D)有一角对应相等的两个菱形相似.   

下列命题是真命题的是（　　 ）

　A.相等的角是对顶角　　    B.两直线被第三条直线所截，内错角相等

　C.若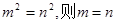　　 D.所有的等边三角形都相似