
题目列表(包括答案和解析)
如图,直线AB与CD相交于点O, OP是∠BOC的平分线,OE⊥AB,OF⊥CD.

(1)图中除直角外,还有相等的角吗?请写出两对:
① ;② .
(2)如果∠AOD=40°,
①那么根据 ,可得∠BOC= 度.
②因为OP是∠BOC的平分线,所以∠COP= ∠
=
度.
∠
=
度.
③求∠POF的度数.
【解析】(1)根据同角的余角相等可知∠COE=∠BOF,利用角平分线的性质可得∠COP=∠BOP,对顶角相等的性质得∠COB=∠AOD.
(2)①根据对顶角相等可得.
②利用角平分线的性质得.
③利用互余的关系可得.
阅读下面材料:
问题:如图①,在△ABC中, D是BC边上的一点,若∠BAD=∠C=2∠DAC=45°,DC=2.求BD的长.
小明同学的解题思路是:利用轴对称,把△ADC进行翻折,再经过推理、计算使问题
得到解决.
(1)请你回答:图中BD的长为 ;
(2)参考小明的思路,探究并解答问题:如图②,在△ABC中,D是BC边上的一点,若∠BAD=∠C=2∠DAC=30°,DC=2,求BD和AB的长.
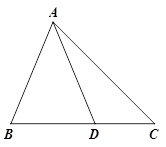
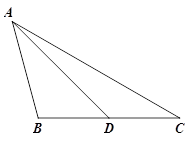
【解析】(1)利用三角形的内角和和角平分线定理进行解答,(2)根据对称的性质、全等三角形的判定和性质以及勾股定理求解
阅读下面材料:
问题:如图①,在△ABC中, D是BC边上的一点,若∠BAD=∠C=2∠DAC=45°,DC=2.求BD的长.
小明同学的解题思路是:利用轴对称,把△ADC进行翻折,再经过推理、计算使问题
得到解决.
(1)请你回答:图中BD的长为 ;
(2)参考小明的思路,探究并解答问题:如图②,在△ABC中,D是BC边上的一点,若∠BAD=∠C=2∠DAC=30°,DC=2,求BD和AB的长.
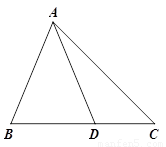
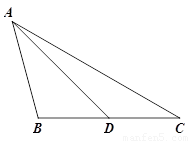
【解析】(1)利用三角形的内角和和角平分线定理进行解答,(2)根据对称的性质、全等三角形的判定和性质以及勾股定理求解
【答案】60°。
【考点】平行线的性质;三角形的外角性质.
【分析】利用三角形的一个外角等于与它不相邻的两个内角的和求出∠3的同位角的度数,再根据两直线平行,同位角相等即可求解.
【解答】如图,∵∠1=130°,∠2=70°,
∴∠4=∠1-∠2=130°-70°=60°,
∵a∥b,
∴∠3=∠4=60°.
故答案为:60°.
【点评】本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,准确识图,理清图中各角度之间的关系是解题的关键.
如图,在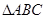 中,AB = AC,D是底边BC的中点,作DE⊥AB于E,DF⊥AC于F,
中,AB = AC,D是底边BC的中点,作DE⊥AB于E,DF⊥AC于F,
求证:DE = DF.

证明: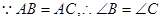 (①
)
(①
)
在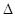 BDE和
BDE和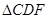 中,
中,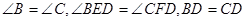 ,
,
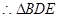 ≌
≌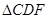 (②
)
(②
)
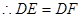 (③
)
(③
)
⑴上面的证明过程是否正确?若正确,请写出①、②和③的推理根据.
⑵请你写出另一种证明此题的方法.
【解析】(1)D是BC的中点,那么AD就是等腰三角形ABC底边上的中线,根据等腰三角形三线合一的特性,可知道AD也是∠BAC的角平分线,根据角平分线的点到角两边的距离相等,那么DE=DF.
(2)连接AD,利用角平分线的性质求证
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com