
题目列表(包括答案和解析)
 3、亲爱的同学们,这是你进入中学后的首次大考,老师送给你一个正方体礼品盒(如图),六面上各有一字,连起来是“预祝考试成功”.其中“预”的对面是“考”,“成”的对面是“功”,则它的平面展开图可能是( )
3、亲爱的同学们,这是你进入中学后的首次大考,老师送给你一个正方体礼品盒(如图),六面上各有一字,连起来是“预祝考试成功”.其中“预”的对面是“考”,“成”的对面是“功”,则它的平面展开图可能是( )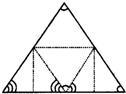 13、亲爱的同学们,在我们的生活中处处有数学的身影,如图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理的结论:“三角形的三个内角和等于
13、亲爱的同学们,在我们的生活中处处有数学的身影,如图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理的结论:“三角形的三个内角和等于| 1 | 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com