
题目列表(包括答案和解析)

图19-1-18
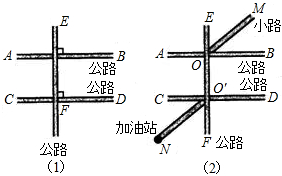
 65、(1)如图(1)所示,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.判断AB与CD的位置关系,并说明理由;
65、(1)如图(1)所示,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.判断AB与CD的位置关系,并说明理由;
| A、a2-b2=(a+b)(a-b) | B、(a+b)2=a2+2ab+b2 | C、(a-b)2=a2-2ab+b2 | D、(a+2b)(a-b)=a2+ab-2b2 |
 油站N的岔道O′N平分∠CO′F,试判断OM与O′N位置关系.
油站N的岔道O′N平分∠CO′F,试判断OM与O′N位置关系.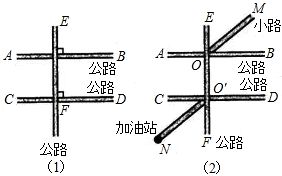
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com