课题活动目的：掌握银行储蓄存款利息的计算方法，学会选择储蓄的最佳期限．

　　课题活动形式：问题研讨课．个人计算与小组讨论相结合．

　　课题参考内容：假设向银行存款1000元，试计算5年后可得的利息金额．存款方式为：(1)5年定期，整存整取；(2)1年定期，每年到期后本息转存；(3)先存2年定期，到期后本息转存3年定期；(4)半年定期，每次到期后本息转存．以上哪种存款方式所得利息最多？试用数学原理说明所得结论．

提示：

(1)到附近银行调查存款的月利率．

即：半年期的利率为：________，

一年期的利率为：________，二年期的利率为：________，

三年期的利率为：________，五年期的利率为：________．

(2)计算公式：

利息＝本金×利率×期限；

本息和＝本金＋本金×利率×期限．

(注：本息和又叫本利和)

一般储蓄扣除利息的20％上缴国家叫做利息税，其中教育储蓄和国库券不扣利息税．

利用课题学习，试计算下列问题：

1．年利率为1.71％，某人存入银行2000元，3年后的利息为________，本息和为________，利息税为________，扣除利息税后本利和为________．

2．一年定期存款，月利率为0.18％，存了100元，一年到期后的利息是多少？利息税是多少？

3．爸爸为小明存了一个3年期的教育储蓄，年利率为2.7％，3年后能取5405元，他开始时存入了多少元？

九年级数学兴趣小组组织了以“等积变形”为主题的课题研究．
第一学习小组发现：如图（1），点A、点B在直线l₁上，点C、点D在直线l₂上，若l₁∥l₂，则S_△ABC=S_△ABD；反之亦成立．
第二学习小组发现：如图（2），点P是反比例函数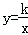上任意一点，过点P作x轴、y轴的垂线，垂足为M、N，则矩形OMPN的面积为定值|k|．

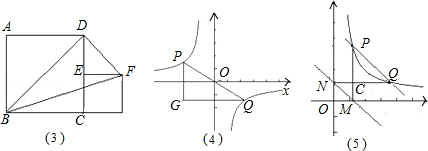
请利用上述结论解决下列问题：
（1）如图（3），四边形ABCD、与四边形CEFG都是正方形点E在CD上，正方形ABCD边长为2，则S_△BDF=　2　．
（2）如图（4），点P、Q在反比例函数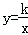图象上，PQ过点O，过P作y轴的平行线交x轴于点H，过Q作x轴的平行线交PH于点G，若S_△PQG=8，则S_△POH=　2　，k=　﹣4　．
（3）如图（5）点P、Q是第一象限的点，且在反比例函数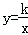图象上，过点P作x轴垂线，过点Q作y轴垂线，垂足分别是M、N，试判断直线PQ与直线MN的位置关系，并说明理由．