如图表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象(分别为正比例函数和一次函数)．两地间的距离是80km．请你根据图象回答或解决下列问题：

(1)谁出发得较早？早多长时间？谁到达乙地较早？早多长时间？

(2)两人在途中行驶的速度分别是多少？

(3)请你分别求出表示自行车和摩托车行驶过程的函数解析式；(不要求写出自变量的取值范围)(因为学生还未学习二元一次方程组解法，所以本题对学生要求较高，但可以通过图象分析出速度，再根据路程与时间的关系列出函数关系式，以下一些类型题可同理解答)；

(4)指出在什么时间段内两车均行驶在途中(不包括端点)、在这一时间段内，请你分别按下列条件列出关于时间x的方程或不等式(不要求化简，也不要求求解)：

①自行车行驶在摩托车前面；

②自行车与摩托车相遇；

③自行车行驶在摩托车后面．

阅读下文，完成文后各题。
羊欣，字敬元，泰山南城人也。父不疑，桂阳太守。欣少靖默，无竞于人，美言笑，善容止。泛览经籍，尤长隶书。不疑初为乌程令，欣时年十二，时王献之为吴兴太守，甚知爱之。献之尝夏月入县，欣著新绢裙昼寝，献之书裙数幅而去。欣本工书，因此弥善。起家辅国参军，府解还家。隆安中，朝廷渐乱，欣优游私门，不复进仕。会稽王世子元显每使欣书，常辞不奉命，元显怒，乃以为其后军府舍人。此职本用寒人，欣意貌恬然，不以高卑见色，论者称焉。欣尝诣领军将军谢混，混拂席改服，然后见之。时混族子灵运在坐，退告族兄瞻曰：“望蔡见羊欣，遂易衣改席。”欣由此益知名。
桓玄辅政，领平西将军，以欣为平西参军，仍转主簿，参预机要。欣欲自疏，时漏密事，玄觉其此意，愈重之，以为楚台殿中郎。谓曰：“尚书政事之本，殿中礼乐所出。卿昔处股肱，方此为轻也。”欣拜职少日，称病自免，屏居里巷，十余年不出。
义熙中，弟徽被遇于高祖，高祖谓咨议参军郑鲜之曰：“羊徽一时美器，世论犹在兄后，恨不识之。”即板欣补右将军刘籓司马，转长史，中军将军道怜谘议参军。出为新安太守。在郡四年，简惠著称。除临川王义庆辅国长史，庐陵王义真车骑谘议参军，并不就。太祖重之，以为新安太守，前后凡十三年，游玩山水，甚得适性。转在义兴，非其好也。顷之，又称病笃自免归。除中散大夫。
素好黄老，常手自书章，有病不服药，饮符水而已。兼善医术，撰《药方》十卷。欣以不堪拜伏，辞不朝觐，高祖、太祖并恨不识之。自非寻省近亲，不妄行诣，行必由城外，未尝入六关。元嘉十九年，卒，时年七十三。
——《宋书•羊欣传》（有删改）
【小题1】对下列句子中加点词的解释，不正确的一项是（    ）

A．欣少靖默，无竞于人竞：争斗

B．称病自免，屏居里巷屏：隐退

C．弟徽被遇于高祖遇：对待

D．自非寻省近亲，不妄行诣诣：去、到

【小题2】下列各组句子中，加点词的意义和用法相同的一组是（    ）

A．献之书裙数幅而去后人哀之而不鉴之

B．不以高卑见色以事秦之心礼天下之奇才

C．殿中礼乐所出不者，若属皆且为所虏

D．转在义兴，非其好也求木之长者，必固其根本

【小题3】下列对原文有关内容的分析和概括，不正确的一项是（    ）

A．羊欣在十二岁时就得到王献之的赏识，王献之在羊欣睡觉的时候，在羊欣的新绢裙上写了几幅字，羊欣的书法也因此得到进一步提高。

B．会稽王世子元显经常让羊欣给他写字，羊欣坚决推辞，因而被贬为军府舍人，但羊欣却能泰然对之。

C．羊欣多次被征召为官，但他却无意于仕途，或辞不就命，或称病自免，即便在任，也常以山水为娱。

D．羊欣平常喜欢黄老之学，经常抄写黄老典籍，即使生病也不吃药，但他却精通医术，还撰写了十卷《药方》。

阅读下列解题过程，借鉴其中一种方法解答后面给出的试题：
问题：某人买13个鸡蛋，5个鸭蛋、9个鹅蛋共用去了9.25元；买2个鸡蛋，4个鸭蛋、3个鹅蛋共用去了3.20元．试问只买鸡蛋、鸭蛋、鹅蛋各一个共需多少元．
分析：设买鸡蛋，鸭蛋、鹅蛋各一个分别需x、y、z元，则需要求x+y+z的值．由题意，知

13x+5y+9z=9.25---(1) 2x+4y+3z=3.20----(2)

；
视x为常数，将上述方程组看成是关于y、z的二元一次方程组，化“三元”为“二元”、化“二元”为“一元”从而获解．
解法1：视x为常数，依题意得

5y+9z=9.25-13x---(3) 4y+3z=3.20-2x----(4)

．
解这个关于y、z的二元一次方程组得

y=0.05+x z=1-2x

．
于是x+y+z=x+0.05+x+1-2x=1.05．
评注：也可以视z为常数，将上述方程组看成是关于x、y的二元一次方程组，解答方法同上，你不妨试试．
分析：视x+y+z为整体，由（1）、（2）恒等变形得5（x+y+z）+4（2x+z）=9.25，4（x+y+z）-（2x+z）=3.20．
解法2：设x+y+z=a，2x+z=b，代入（1）、（2）可以得到如下关于a、b的二元一次方
程组

5a+4b=9.25---(5) 4a-b=3.20----(6)

．
由⑤+4×⑥，得21a+22.05，a=1.05．
评注：运用整体的思想方法指导解题．视x+y+z，2x+z为整体，令a=x+y+z，b=2x+z，代入①、②将原方程组转化为关于a、b的二元一次方程组从而获解．
请你运用以上介绍的任意一种方法解答如下数学竞赛试题：
购买五种教学用具A₁、A₂、A₃、A₄、A₅的件数和用钱总数列成下表：

那么，购买每种教学用具各一件共需多少元？

阅读下列解题过程，借鉴其中一种方法解答后面给出的试题：

    问题：某人买13个鸡蛋，5个鸭蛋、9个鹅蛋共用去了9.25元；买2个鸡蛋，4个鸭蛋、3个鹅蛋共用去了3.20元．试问只买鸡蛋、鸭蛋、鹅蛋各一个共需多少元．

    分析：设买鸡蛋，鸭蛋、鹅蛋各一个分别需x、y、z元，则需要求x+y+z的值．由题意，知；

    视为常数，将上述方程组看成是关于y、z的二元一次方程组，化“三元”为“二元”、化“二元”为“一元”从而获解．

解法1：视为常数，依题意得

解这个关于y、z的二元一次方程组得

  于是．

    评注：也可以视z为常数，将上述方程组看成是关于、的二元一次方程组，解答方法同上，你不妨试试．

分析：视为整体，由(1)、(2)恒等变形得

，

．

    解法2：设，，代入(1)、(2)可以得到如下关于、的二元一次方

程组

由⑤+4×⑥，得，．

    评注：运用整体的思想方法指导解题．视，为整体，令，，代人①、②将原方程组转化为关于、的二元一次方程组从而获解．

    请你运用以上介绍的任意一种方法解答如下数学竞赛试题：

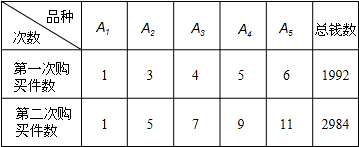
购买五种教学用具A₁、A₂、A₃、A₄、A₅的件数和用钱总数列成下表：

品名 次数	A1	A2	A3	A4	A5	总钱数
第一次购 买件数	l	3	4	5	6	1992
第二次购   买件数	l	5	7	9	11	2984

  那么，购买每种教学用具各一件共需多少元?