解：（1）由抛物线C₁：得顶点P的坐标为（2，5）………….1分

∵点A（－1，0）在抛物线C₁上∴.………………2分

（2）连接PM，作PH⊥x轴于H，作MG⊥x轴于G..

∵点P、M关于点A成中心对称,

∴PM过点A，且PA＝MA..

∴△PAH≌△MAG..

∴MG＝PH＝5，AG＝AH＝3.

∴顶点M的坐标为（，5）.………………………3分

∵抛物线C₂与C₁关于x轴对称，抛物线C₃由C₂平移得到

∴抛物线C₃的表达式.  …………4分

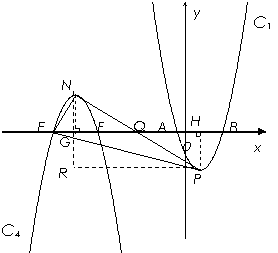
（3）∵抛物线C₄由C₁绕x轴上的点Q旋转180°得到

∴顶点N、P关于点Q成中心对称.

 由（2）得点N的纵坐标为5.

设点N坐标为（m，5），作PH⊥x轴于H，作NG⊥x轴于G，作PR⊥NG于R.

∵旋转中心Q在x轴上,

∴EF＝AB＝2AH＝6.

 ∴EG＝3，点E坐标为（，0），H坐标为（2，0），R坐标为（m，－5）.

根据勾股定理，得

     

  

       

①当∠PNE＝90º时，PN²+ NE²＝PE²，

解得m＝，∴N点坐标为（，5）

②当∠PEN＝90º时，PE²+ NE²＝PN²，

解得m＝，∴N点坐标为（，5）.

③∵PN＞NR＝10＞NE，∴∠NPE≠90º  ………7分

综上所得，当N点坐标为（，5）或（，5）时，以点P、N、E为顶点的三角形是直角三角形．…………………………………………………………………………………8分