阅读下列材料：

解方程．

解：方程两边同乘x－2，约去分母，得

1＝x－1－3(x－2)

解这个整式方程，得x＝2．

所以，原方程的解为x＝2．

根据以上材料，回答下列问题：

(1)以上解答是否有错误，若有错误，指出错误，并改正；

(2)请你根据这个方程的特点，用另外一种方法解答．

下列说法中，正确的说法有

①对角线互相平分且相等的四边形是菱形；

②一元二次方程x²－3x－4＝0的根是x₁＝4，x₂＝－1；

③依次连接任意一个四边形各边中点所得的四边形是平行四边形；

④一元一次不等式2x＋5＜11的正整数解有3个；

⑤在数据1，3，3，0，2中，众数是3，中位数是3．

A．1个

B．2个

C．3个

D．4个

(1)阅读下面材料：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为|AB|．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|＝|OB|＝|b|＝|a－b|当A、B两点都不在原点时，

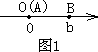
①如图2，点A、B都在原点的右边|AB|＝|OB|－|OA|＝|b|－|a|＝b－a＝|a－b|；

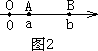
②如图3，点A、B都在原点的左边，|AB|＝|OB|－|OA|＝|b|－|a|＝b－a＝|a－b|；

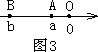
③如图4，点A、B在原点的两边，|AB|＝|OB|－|OA|＝|b|－|a|＝－b－(－a)＝|a－b|；综上，数轴上A、B两点之间的距离|AB|＝|a－b|．

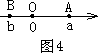
(2)回答下列问题：

①数轴上表示2和5的两点之间的距离是________，数轴上表示－2和－5的两点之间的距离是________，

数轴上表示1和－3的两点之间的距离是________；

②数轴上表示x和－1的两点A和B之间的距离是________，如果|AB|＝3，那么x________；

③当代数式|x＋2|十|x－5|取最小值时，相应的x的取值范围是________

④解方程∣x＋2∣＋∣x－5∣＝9

请阅读下列材料：

问题：已知方程x²＋x－1＝0，求一个一元二次方程，使它的根分别是已知方程根的2倍．

解：设所求方程的根为y，则y＝2x所以x＝．

把x＝代入已知方程，得()²＋－1＝0

化简，得y²＋2y－4＝0

故所求方程为y²＋2y－4＝0．

这种利用方程根的代换求新方程的方法，我们称为“换根法”．

请用阅读村料提供的“换根法”求新方程(要求：把所求方程化为一般形式)：

(1)已知方程x²＋x－2＝0，求一个一元二次方程，使它的根分别为己知方程根的相反数，则所求方程为：________；

(2)己知关于x的一元二次方程ax²＋bx＋c＝0有两个不等于零的实数根，求一个一元二次方程，使它的根分别是己知方程根的倒数．