
题目列表(包括答案和解析)
(本题12分) 如果一个正整数能够表示为两个连续的偶数的平方差,那么称这个正整数为“神秘数” .如4=22-02;12=42-22;20=62-42.因此4、12、20这三个数都是神秘数.
(1)请你写出50以内的两个神秘数(除4、12、20外),并判断2012是否是神秘数?(不要说明理由)
(2)设两个连续偶数为2 +2和2
+2和2 (其中
(其中 为非负整数) ,由这两个连续偶数构造的神秘数是4的倍数吗?说明理由.
为非负整数) ,由这两个连续偶数构造的神秘数是4的倍数吗?说明理由.
(3)试说明:两个连续奇数的平方差(取正数)不是神秘数.
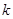 +2和2
+2和2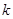 (其中
(其中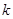 为非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?说明理由.(本题12分) 如果一个正整数能够表示为两个连续的偶数的平方差,那么称这个正整数为“神秘数” .如4=22-02;12=42-22;20=62-42.因此4、12、20这三个数都是神秘数.
(1)请你写出50以内的两个神秘数(除4、12、20外),并判断2012是否是神秘数?(不要说明理由)
(2)设两个连续偶数为2![]() +2和2
+2和2![]() (其中
(其中![]() 为非负整数) ,由这两个连续偶数构造的神秘数是4的倍数吗?说明理由.
为非负整数) ,由这两个连续偶数构造的神秘数是4的倍数吗?说明理由.
(3)试说明:两个连续奇数的平方差(取正数)不是神秘数.
 +2和2
+2和2 (其中
(其中 为非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?说明理由. (本题12分) 如果一个正整数能够表示为两个连续的偶数的平方差,那么称这个正整数为“神秘数”.如4=22-02;12=42-22;20=62-42.因此4、12、20这三个数都是神秘数.
(1)请你写出50以内的两个神秘数(除4、12、20外),并判断2012是否是神秘数?(不要说明理由)
(2)设两个连续偶数为2 +2和2
+2和2 (其中
(其中 为非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?说明理由.
(3)试说明:两个连续奇数的平方差(取正数)不是神秘数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com