
题目列表(包括答案和解析)
阅读理解题:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.那么形如a+bi(a,b为实数)的数就叫做复数, a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:(2+i)+(3-4i)=5-3i.
【小题1】填空:i3=_____,i4="_______" ;
【小题2】计算:① ;②
;② ;
;
【小题3】若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:
已知:(x+y)+3i=(1-x)-yi,(x,y为实数),求x,y的值.
【小题4】试一试:请利用以前学习的有关知识将 化简成a+bi的形式
化简成a+bi的形式
阅读理解题:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.那么形如a+bi(a,b为实数)的数就叫做复数, a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:(2+i)+(3-4i)=5-3i.
1.填空:i3=_____,i4=_______ ;
2.计算:① ;②
;② ;
;
3.若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:
已知:(x+y)+3i=(1-x)-yi,(x,y为实数),求x,y的值.
4.试一试:请利用以前学习的有关知识将 化简成a+bi的形式
化简成a+bi的形式
阅读理解题:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.那么形如a+bi(a,b为实数)的数就叫做复数, a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:(2+i)+(3-4i)=5-3i.
(1)填空:i3=_____,i4=_______ ;
(2)计算:①![]() ;②
;②![]() ;
;
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:
已知:(x+y)+3i=(1-x)-yi,(x,y为实数),求x,y的值.
(4)试一试:请利用以前学习的有关知识将![]() 化简成a+bi的形式.
化简成a+bi的形式.
 ;②
;②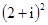 ;
;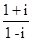 化简成a+bi的形式
化简成a+bi的形式| 1+i | 1-i |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com