
题目列表(包括答案和解析)
 如图,已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0)两点,且过点(-1,16),抛物线的顶点是点C,对称轴与x轴的交点为点D,原点为点O.在y轴的正半轴上有一动点N,使以A、O、N这三点为顶点的三角形与以C、A、D这三点为顶点的三角形相似.求:
如图,已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0)两点,且过点(-1,16),抛物线的顶点是点C,对称轴与x轴的交点为点D,原点为点O.在y轴的正半轴上有一动点N,使以A、O、N这三点为顶点的三角形与以C、A、D这三点为顶点的三角形相似.求:
如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16 m,AE=8 m,抛物线的顶点C到ED的距离是11 m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.

(1)求抛物线的解析式;
(2)已知从某时刻开始的40 h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数关系h=-![]() (t-19)2+8(0≤t≤40)且当水面到顶点C的距离不大于5 m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
(t-19)2+8(0≤t≤40)且当水面到顶点C的距离不大于5 m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
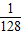 (t-19)2+8(0≤t≤40),且当水面到顶点C的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
(t-19)2+8(0≤t≤40),且当水面到顶点C的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?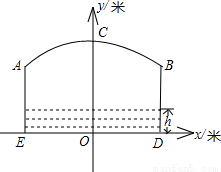
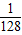 (t-19)2+8(0≤t≤40),且当水面到顶点C的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
(t-19)2+8(0≤t≤40),且当水面到顶点C的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?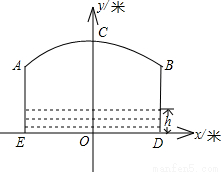
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com