（2013•苏州一模）如图（1），在Rt△AOB中，∠AOB=90°，∠B=30°且AO=1，延长BA、BO，点C为BA延长线上的一动点，以每秒1个单位长度的速度从点A开始沿射线BA向上移动，作等边△CDE，点D和点E都在射线BO上，
（1）求BO的长；
（2）若半径为2

3

的⊙M与射线BO、射线BA相切于点G、F，求当等边△CDE的边CE与⊙M相切时的边长；
（3）以O为坐标原点，直线OB、OA为x轴、y轴建立如图（2）所示的直角坐标系，若以点C为顶点的抛物线y=a（x-m）2+n经过点E．⊙M与x轴、射线BA都相切，其半径为3（1-

3

）a．问点C移动多少秒时，等边△CDE的边CE第一次与⊙M相切？

23、如图，已知∠MAN=120°，AC平分∠MAN．B、D分别在射线AN、AM上．
（1）在图（1）中，当∠ABC=∠ADC=90°时，求证：AD+AB=AC．
（2） 若把（1）中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°，其他条件不变，如图（2）所示．则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．

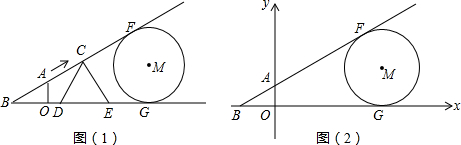
（2013•杭州一模）如图（1）所示，E为矩形ABCD的边AD上一点，动点P、Q同时从点B出发，点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止，点Q以2cm/秒的速度沿BC运动到点C时停止．设P、Q同时出发t秒时，△BPQ的面积为ycm²．已知y与t的函数关系图象如图；
（2）（其中曲线OG为抛物线的一部分，其余各部分均为线段），则下列结论：
①当0＜t≤5时，y=

4

5

t²；②当t=6秒时，△ABE≌△PQB；③cos∠CBE=

1

2

；④当t=

29

2

秒时，△ABE∽△QBP；
其中正确的是（　　）

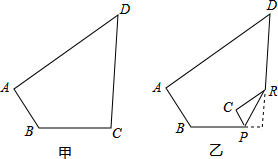如图，（甲）是四边形纸片ABCD，其中∠B=130°，∠D=50°．若将其右下角向内折出△PCR，恰使CP∥AB，RC∥AD，如图（乙）所示，则∠C=．