
题目列表(包括答案和解析)
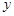 与
与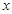 之间的函数关系式及其定义域.
之间的函数关系式及其定义域.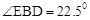 ?如果存在,求出AD的长度;如果不存在,请说明理由.
?如果存在,求出AD的长度;如果不存在,请说明理由.| 50 |

| 50 |
| 50 |
| 2 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
 劳技课上,同学们领到了一根长方形木条(图3),班长倡议:我们用锯子分割一下,然后用强力胶粘起来,为数学老师做一把有一个角30°的直角三角板.于是同学们分成甲乙两个组,进行探究:
劳技课上,同学们领到了一根长方形木条(图3),班长倡议:我们用锯子分割一下,然后用强力胶粘起来,为数学老师做一把有一个角30°的直角三角板.于是同学们分成甲乙两个组,进行探究:| 3 |
| 3 |
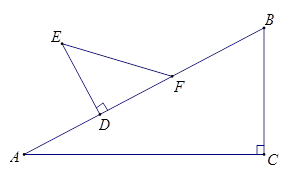
 (2014•宝山区一模)如图△ABC中,∠C=90°,∠A=30°,BC=5cm;△DEF中,∠D=90°,∠E=45°,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动(如图).在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动至点F与点B重合为止).
(2014•宝山区一模)如图△ABC中,∠C=90°,∠A=30°,BC=5cm;△DEF中,∠D=90°,∠E=45°,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动(如图).在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动至点F与点B重合为止).湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com