
题目列表(包括答案和解析)
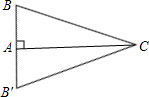 要测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点B′,使∠ACB′=∠ACB,这时只要量出AB′的长,就知道AB的长.
要测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点B′,使∠ACB′=∠ACB,这时只要量出AB′的长,就知道AB的长.
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

 ∠A. 说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____. 根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.根据角平分线的意义,可知∠2+∠3=
∠A. 说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____. 根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.根据角平分线的意义,可知∠2+∠3= (∠EBC+∠FCB)=
(∠EBC+∠FCB)= (180°+∠_____)=90°+
(180°+∠_____)=90°+ ∠_______.所以∠BGC=180°-(∠2+∠3)=90°-∠____
∠_______.所以∠BGC=180°-(∠2+∠3)=90°-∠____ ∠A.
∠A.

请完成下面的说明:
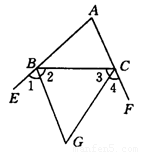
【小题1】如图①所示,△ABC的外角平分线交于G,试说明∠BGC=90°-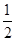 ∠A. 说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____. 根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.根据角平分线的意义,可知∠2+∠3=
∠A. 说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____. 根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.根据角平分线的意义,可知∠2+∠3=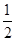 (∠EBC+∠FCB)=
(∠EBC+∠FCB)=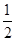 (180°+∠_____)=90°+
(180°+∠_____)=90°+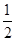 ∠_______.所以∠BGC=180°-(∠2+∠3)=90°-∠____
∠_______.所以∠BGC=180°-(∠2+∠3)=90°-∠____
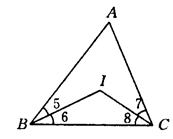
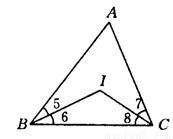
【小题2】如图②所示,若△ABC的内角平分线交于点I,试说明∠BIC=90°+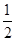 ∠A.
∠A.
【小题3】用(1),(2)的结论,你能说出∠BGC和∠BIC的关系吗?(直接写出结论)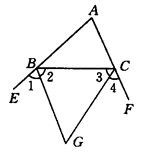
请完成下面的说明:
1.如图①所示,△ABC的外角平分线交于G,试说明∠BGC=90°-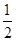 ∠A. 说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____. 根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.根据角平分线的意义,可知∠2+∠3=
∠A. 说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____. 根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.根据角平分线的意义,可知∠2+∠3=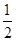 (∠EBC+∠FCB)=
(∠EBC+∠FCB)=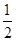 (180°+∠_____)=90°+
(180°+∠_____)=90°+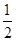 ∠_______.所以∠BGC=180°-(∠2+∠3)=90°-∠____
∠_______.所以∠BGC=180°-(∠2+∠3)=90°-∠____
2.如图②所示,若△ABC的内角平分线交于点I,试说明∠BIC=90°+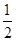 ∠A.
∠A.
3.用(1),(2)的结论,你能说出∠BGC和∠BIC的关系吗?(直接写出结论)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com