练习册

  • 练习册
  • 试题
    如图1.点P有△ABC内.则下列叙述正确的是( ) A. B.°>° C.°<° D.不能确定 D A 4．已知.如图.AB∥CD.∠A=700.∠B=400.则∠ACD=( ) A. 550 B. 700 C. 400 D. 1100 【查看更多】

     

    题目列表(包括答案和解析)

    在Rt△ABC中，∠CAB=90°，AB=AC．
    （1）如图①，过点A在△ABC外作直线MN，BM⊥MN于M，CN⊥MN于N．
    ①判断线段MN、BM、CN之间有何数量关系，并证明；
    ②若AM=a，BM=b，AB=c，试利用图①验证勾股定理a2+b2=c2；
    （2）如图②，过点A在△ABC内作直线MN，BM⊥MN于M，CN⊥MN于N，判断线段MN、BM、CN之间有何数量关系？（直接写出答案）

    查看答案和解析>>

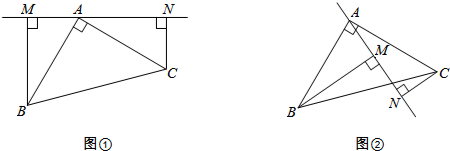
    如图，当点O是△ABC内的一动点，D、E、F、G分别是AB、BO、CO、AC的中点，连结DE、EF、FG、GD，
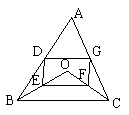    （1）求证：四边形DEFG是平行四边形。
    （2）当点O在△ABC外部时，其它条件不变，上面的结论是否成立？为什么？
    （3）要使DEFG是矩形，点O的位置有何特点？(不用证明)

    查看答案和解析>>

    （1）如图1，点O是△ABC内任意一点，G、D、E分别为AC、OA、OB的中点，F为BC上一动点，问四边形GDEF能否为平行四边形？若可以，指出F点位置，并给予证明；
    （2）（填空，使下列命题成立，不要求证明）如图3，点E、F、G、H分别为AB、BC、CD、DA的中点．
    当
     
    时，四边形EFGH为矩形；
    当
     
    时，四边形EFGH为菱形；
    当
     
    时，四边形EFGH为正方形．
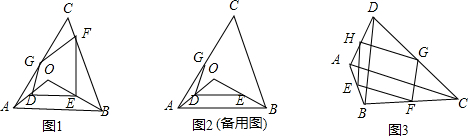
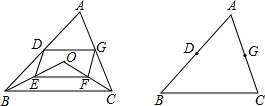    精英家教网

    查看答案和解析>>

    （2013•高淳县一模）如图①，若点P是△ABC内或边上一点，且∠BPC=2∠A，则称点P是△ABC内∠A的二倍角点．
    （1）如图②，点O等边△ABC的外心，连接OB、OC．
    ①求证：点O是△ABC内∠A的一个二倍角点；
    ②作△BOC的外接圆，求证：弧BOC上任意一点（B、C除外）都是△ABC内∠A的二倍角点．
    （2）如图③，在△ABC的边AB上求作一点M，使点M是△ABC内∠A的一个二倍角点（要求用尺规作图，保留作图痕迹，并写出作法）．
    （3）在任意三角形形内，是否存在一点P同时为该三角形内三个内角的二倍角点？请直接写出结论，不必说明理由．

    查看答案和解析>>

    精英家教网点O是三角形ABC所在平面内一动点，连接OB、OC，并将AB、OB、OC、AC中点D、E、F、G，依次连接起来，设DEFG能构成四边形．
    （1）如图，当点O在△ABC内时，求证：四边形DEFG是平行四边形；
    （2）当点O在△ABC外时，（1）的结论是否成立？（画出图形，指出结论，不需说明理由；）
    （3）若四边形DEFG是菱形，则点O的位置应满足什么条件？试说明理由．

    查看答案和解析>>


    同步练习册答案