
题目列表(包括答案和解析)
如图,直线y=-x+b(b>0)与双曲线![]() (x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N;有以下结论:
(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N;有以下结论:
①OA=OB
②△AOM≌△BON
③若∠AOB=45°,则S△AOB=k
④当AB=![]() 时,ON-BN=1;
时,ON-BN=1;
其中结论正确的个数为

A.1
B.2
C.3
D.4
如图,直线y=-x+b(b>0)与双曲线y=![]() (x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N;有以下结论:
(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N;有以下结论:
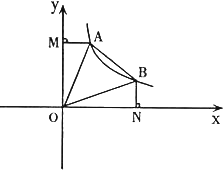
①OA=OB
②△AOM≌△BON.
③若∠AOB=45°.则S△AOB=k
④当AB=![]() 时,ON=BN=l;
时,ON=BN=l;
其中结论正确的个数为
A.1
B.2
C.3
D.4
先阅读下面一段材料,再完成后面的问题:
材料 过抛物线y=ax2(a>0)的对称轴上一点(0,-![]() ),作对称轴的垂线l,则抛物线上任意一点P到点F(0,
),作对称轴的垂线l,则抛物线上任意一点P到点F(0,![]() )的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0,
)的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0,![]() ).
).
问题 若直线y=kx+b交抛物线y=![]() x2于A、B两点,AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图).
x2于A、B两点,AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图).
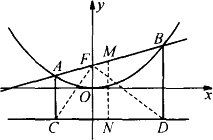
(1)求抛物线y=![]() x2的焦点F的坐标;
x2的焦点F的坐标;
(2)求证:直线AB过焦点时,CF⊥DF;
(3)当直线AB过点(-1,0),且以线段AB为直径的圆与准线l相切时,求这条直线对应的函数解析式.
已知:以原点O为圆心、5为半径的半圆与y轴交于A、G两点,AB与半圆相切于点A,点B的坐标为(3,yB)(如图1);过半圆上的点C(xC,yC)作y轴的垂线,垂足为D;Rt△DOC的面积等于![]() .
.
(1
)求点C的坐标;(2
)①命题撊缤-2,以y轴为对称轴的等腰梯形MNPQ与M1N1P1Q1的上底和下底都分别在同一条直线上,NP∥MQ,PQ∥P1Q1 ,且NP>MQ.设抛物线y=a0x2+h0过点P、Q,抛物线y=a1x2+h1过点P1、Q1,则h0>h1斒钦婷?猓?肽阋-Q(3,5)、P(4,3)和Q1(p,5)、P1(p+1,3)为例进行验证;②当图1中的线段BC在第一象限时,作线段BC关于y轴对称的线段FE,连接BF、CE,点T是线段BF上的动点(如图3);设K是过T、B、C三点的抛物线y=ax2+bx+c的顶点,求K的纵坐标yK的取值范围.

若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=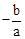 ,x1•x2=
,x1•x2=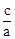 .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:AB=|x1-x2|=
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:AB=|x1-x2|=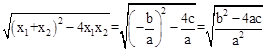
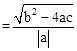 。
。
参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值.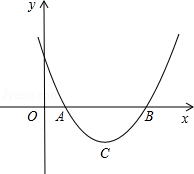
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com