数学学习总是如数学知识自身的生长历史一样,往往起源于猜测中的发现,我们所发现的不一定对,但是当利用我们已有的知识作为推理的前提论证之后,当所发现的在逻辑上没有矛盾之后,就可以作为新的推理的前提,数学中称之为定理.
(1)尝试证明:
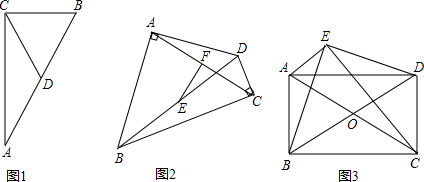
等腰三角形的探索中借助折纸发现:直角三角形斜边上的中线等于斜边的一半.但是当时并未说明这个结论的合理.现在我们学些了矩形的判定和性质之后,就可以解决这个问题了.如图1若在Rt△ABC中CD是斜边AB的中线,则
CD=AB,你能用矩形的性质说明这个结论吗?请说明.
(2)迁移运用:利用上述结论解决下列问题:
①如图2所示,四边形ABCD中,∠BAD=90°,∠DCB=90°,EF分别是BD、AC的中点,请你说明EF与AC的位置关系.
②如图3所示,?ABCD中,以AC为斜边作Rt△ACE,∠AEC=90°,且∠BED=90°,试说明平行四边形ABCD是矩形.

