
题目列表(包括答案和解析)
如图正方形ABCD和正方形EFGH,F和B重合,EF在AB上,连DH(本题14分)
⑴、由图⑴易知,
①线段AE=CG, AE和CG所在直线互相垂直,且此时易求得② 。
。
⑵、若把正方形EFGH绕F点逆时针旋转 度(图2),⑴中的两个结论是否仍然成立?若成立,选择其中一个加以证明,若不成立,请说明理由。
度(图2),⑴中的两个结论是否仍然成立?若成立,选择其中一个加以证明,若不成立,请说明理由。
⑶、若把图⑴中的正方形EFGH沿BD方向以每秒1cm的速度平移,设平移时间为x秒,正方形ABCD和正方形EFGH的边长分别为5cm和1cm,
①在平移过程中,△AFH是否会成为等腰三角形?若能求出x的值,若不能,说明理由.
②在平移过程中,△AFH是否会成为等边三角形?若能求出x的值,若不能,设正方形ABCD和正方形EFGH的边长分别为acm和bcm,则当a、b满足什么关系时,△AFH可以成为等边三角形.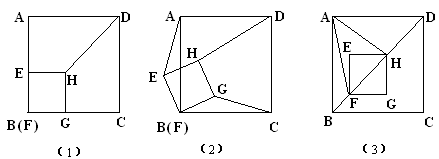
如图正方形ABCD和正方形EFGH,F和B重合,EF在AB上,连DH(本题14分)
⑴、由图⑴易知,
①线段AE=CG, AE和CG所在直线互相垂直,且此时易求得② 。
。
⑵、若把正方形EFGH绕F点逆时针旋转 度(图2),⑴中的两个结论是否仍然成立?若成立,选择其中一个加以证明,若不成立,请说明理由。
度(图2),⑴中的两个结论是否仍然成立?若成立,选择其中一个加以证明,若不成立,请说明理由。
⑶、若把图⑴中的正方形EFGH沿BD方向以每秒1cm的速度平移,设平移时间为x秒,正方形ABCD和正方形EFGH的边长分别为5cm和1cm,
①在平移过程中,△AFH是否会成为等腰三角形?若能求出x的值,若不能,说明理由.
②在平移过程中,△AFH是否会成为等边三角形?若能求出x的值,若不能,设正方形ABCD和正方形EFGH的边长分别为acm和bcm,则当a、b满足什么关系时,△AFH可以成为等边三角形.

 。
。 度(图2),⑴中的两个结论是否仍然成立?若成立,选择其中一个加以证明,若不成立,请说明理由。
度(图2),⑴中的两个结论是否仍然成立?若成立,选择其中一个加以证明,若不成立,请说明理由。
如图所示,正方形EFGH是由正方形ABCD平移得到的,则有
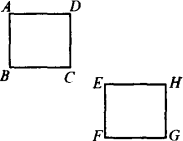
A.点E和B对应
B.线段AD和EH对应
C.线段AC和FH对应
D.∠B和∠D对应

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com