
题目列表(包括答案和解析)
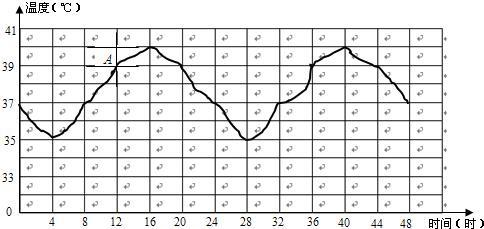
 12、骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化,其体温(℃)与时间(时)之间的关系如图所示.若y(℃)表示0时到t时内骆驼体温的温差(即0时到t时最高温度与最低温度的差).则y与t之间的函数关系用图象表示,大致正确的是( )
12、骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化,其体温(℃)与时间(时)之间的关系如图所示.若y(℃)表示0时到t时内骆驼体温的温差(即0时到t时最高温度与最低温度的差).则y与t之间的函数关系用图象表示,大致正确的是( )
| |||||
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com