练习册

  • 练习册
  • 试题
    如图.在△ABC中.AD.CE是两条高.连结DE.如果BE=2.AE=3.CE=4在不添加任何辅助线和字母的条件下.写出三个正确的结论(要求:分别为边 的关系.角的关系.三角形相似等).并对其中一个结论给予证明. C D A E B 【查看更多】

     

    题目列表(包括答案和解析)

    如图，在△ABC中，AB=AC，AD、BE是△ABC的两条高，连接DE交AB于点O，则下列结论中，
    ①ED=
    1
    2
    BC；②∠BAC=2∠EBD=2∠BED；③△AOD∽△BOE；④CB2=2CA•CE；⑤图中相似三角形只有三对．
    正确的有（　　）
    A、1个B、2个C、3个D、4

    查看答案和解析>>

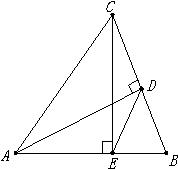    30、如图，在△ABC中，AD、CE是两条高，连接DE．如果BE=2，EA=3，CE=4，在不添加任何辅助线和字母的条件下，写出三个正确的结论（要求：分别为边的关系、角的关系、三角形相似等），并对其中一个结论给予证明．

    查看答案和解析>>

    如图，在△ABC中，AD、CE是两条高，连接DE，如果BE=2，EA=3，CE=4，在不添加任何辅助线和字母的条件下，请写出三个正确结论   （要求：分别为边的关系，角的关系，三角形相似的关系），并对其中三角形相似的结论给予证明．
    边的关系
    AC=AB
    AC=AB
    ；
    角的关系
    ∠CAB=∠B
    ∠CAB=∠B
    ；
    三角形相似的关系
    △BED∽△BCA
    △BED∽△BCA
    ．

    查看答案和解析>>

      (本小题满分12分)

     1. (1)观察发现

        如(a)图，若点A，B在直线同侧，在直线上找一点P，使AP+BP的值最小．

        做法如下：作点B关于直线的对称点，连接，与直线的交点就是所求的点P

        再如(b)图，在等边三角形ABC中，AB=2，点E是AB的中点，AD是高，在AD上找一点P，使BP+PE的值最小．

    做法如下：作点B关于AD的对称点，恰好与点C重合，连接CE交AD于一点，则这点就是所求的点P，故BP+PE的最小值为       ． (2分)

            

     

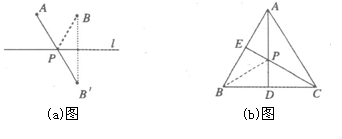
    2.(2)实践运用

       如图，菱形ABCD的两条对角线分别长6和8，点P是对角线AC上的一个动点，点M、N分别是边AB、BC的中点，求PM+PN的最小值。(5分)

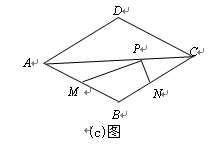
    3.(3)拓展延伸

        如(d)图，在四边形ABCD的对角线AC上找一点P，使∠APB=∠APD．保留作图痕迹，不必写出作法．  (5分)

     

    查看答案和解析>>

    如图，在△ABC中，AD、CE是两条高，连结DE，如果BE=2，EA=3，CE=4，在不添加任何辅助线和字母的条件下，请写出三个正确结论  （要求：分别为边的关系，角的关系，三角形相似的关系），并对其中三角形相似的结论给予证明.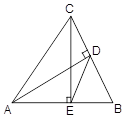

    边的关系                       ;
    角的关系                       ;
    三角形相似的关系                          .
    证明:

    查看答案和解析>>


    同步练习册答案