
题目列表(包括答案和解析)

图1是一个长为2 ,宽为2
,宽为2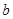 的长方形,沿图中虚线剪开,可分成四块小长方形.
的长方形,沿图中虚线剪开,可分成四块小长方形.
(1)求出图1的长方形面积;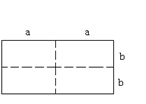
(2)将四块小长方形拼成一个图2的正方形.利用阴影部分面积的不同表示方法,直接写出代数式(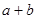 )2、(
)2、( )2、
)2、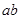 之间的等量关系;
之间的等量关系;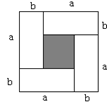
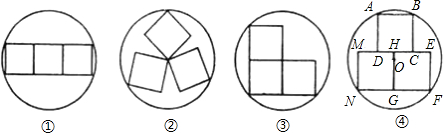
(3)把四块小长方形不重叠地放在一个长方形的内部(如图3),未被覆盖的部分用
阴影表示.求两块阴影部分的周长和(用含 、
、 的代数式表示).
的代数式表示).
图1是一个长为2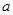 ,宽为2
,宽为2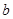 的长方形,沿图中虚线剪开,可分成四块小长方形.
的长方形,沿图中虚线剪开,可分成四块小长方形.
(1)求出图1的长方形面积;
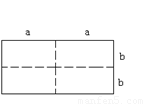
(2)将四块小长方形拼成一个图2的正方形.利用阴影部分面积的不同表示方法,直接写出代数式(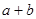 )2、(
)2、(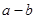 )2、
)2、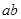 之间的等量关系;
之间的等量关系;
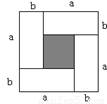
(3)把四块小长方形不重叠地放在一个长方形的内部(如图3),未被覆盖的部分用
阴影表示.求两块阴影部分的周长和(用含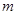 、
、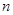 的代数式表示).
的代数式表示).


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com