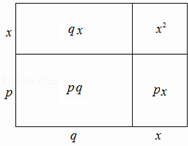
如图，大长方形是由四个小长方形拼成的，请根据此图填空：x²+（p+q）x+pq=x²+px+qx+pq=（　　）（　　）．

说理验证

事实上，我们也可以用如下方法进行变形：

x²+（p+q）x+pq=x²+px+qx+pq=（x²+px）+（）=　　=（　　）（　　）．

于是，我们可以利用上面的方法进行多项式的因式分解．

尝试运用

例题 把x²+3x+2分解因式．

解：x²+3x+2=x²+（2+1）x+2×1=（x+2）（x+1）．

请利用上述方法将下列多项式分解因式：

（1）x²﹣7x+12；            （2）（y²+y）²+7（y²+y）﹣18．

如图，大长方形是由四个小长方形拼成的，请根据此图填空：x²+（p+q）x+pq=x²+px+qx+pq=（　　）（　　）．
说理验证
事实上，我们也可以用如下方法进行变形：
x²+（p+q）x+pq=x²+px+qx+pq=（x²+px）+（）=　　=（　　）（　　）．
于是，我们可以利用上面的方法进行多项式的因式分解．
尝试运用
例题 把x²+3x+2分解因式．
解：x²+3x+2=x²+（2+1）x+2×1=（x+2）（x+1）．
请利用上述方法将下列多项式分解因式：
（1）x²﹣7x+12；            （2）（y²+y）²+7（y²+y）﹣18．

观察猜想
如图，大长方形是由四个小长方形拼成的，请根据此图填空：x²+（p+q）x+pq=x²+px+qx+pq=（______）（______）．
说理验证
事实上，我们也可以用如下方法进行变形：
x²+（p+q）x+pq=x²+px+qx+pq=（x²+px）+（qx+pq）=______=（______）（______）．
于是，我们可以利用上面的方法进行多项式的因式分解．
尝试运用
例题　把x²+3x+2分解因式．
解：x²+3x+2=x²+（2+1）x+2×1=（x+2）（x+1）．
请利用上述方法将下列多项式分解因式：
（1）x²-7x+12；　　　　　　 （2）（y²+y）²+7（y²+y）-18．