
题目列表(包括答案和解析)
阅读下列方法:为了找出序列3、8、15、24、35、48、……的规律,我们有一种“因式分解法”。如下表:
| 项 | 1 | 2 | 3 | 4 | 5 | 6 | …… | n |
| 值 | 3 | 8 | 15 | 24 | 35 | 48 | …… |
分解因式: 1×3 1×8 1×15 1×24 1×35 1×48
2×4 3×5 2×12 5×7 2×24
4×6 3×16
4×12
6×8
因此,我们得到第n项是n(n+2),请你利用上述方法,说出序列:0、5、12、21、32、45、……的第n项是 。
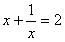 ,求
,求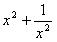 的值”。某同学是这样解答的:
的值”。某同学是这样解答的: 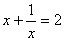 ,所以
,所以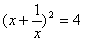 ,
, 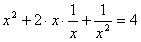 ,所以
,所以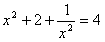 ,
,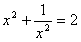 。仿照此法或者用该结论,(也可不用此法,用你自己想到的方法作答)
。仿照此法或者用该结论,(也可不用此法,用你自己想到的方法作答)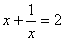
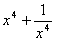 、
、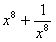 、
、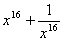 的值;
的值;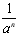 (a≠0).无论从仿照同底数幂的除法公式来分析,还是仿照分式的约分来分析,这种规定都是合理的.正是有了这种规定,指数的范围由非负数扩大到全体整数,概念的扩充与完善使我们解决问题的路更宽了。例如a2·a-3=a2+(-3)=a-1=
(a≠0).无论从仿照同底数幂的除法公式来分析,还是仿照分式的约分来分析,这种规定都是合理的.正是有了这种规定,指数的范围由非负数扩大到全体整数,概念的扩充与完善使我们解决问题的路更宽了。例如a2·a-3=a2+(-3)=a-1=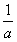 ,数的发展经历了漫长的过程,其实人们早就发现了非实数的数.人们规定:i2=-1,这里数i类似于实数单位1,它的运算法则与实数运算法则完全类似:2i+
,数的发展经历了漫长的过程,其实人们早就发现了非实数的数.人们规定:i2=-1,这里数i类似于实数单位1,它的运算法则与实数运算法则完全类似:2i+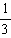 i=
i=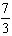 i(注意:由于非实数与实数单位不同,因此像2+i之类的运算便无法继续进行,2+i就是一个非实数的数),6·0.5i=3i;2i·3i=6i2=-6;(3i)2=-9;-4的平方根为±2i;如果x2=-7,那么x=±
i(注意:由于非实数与实数单位不同,因此像2+i之类的运算便无法继续进行,2+i就是一个非实数的数),6·0.5i=3i;2i·3i=6i2=-6;(3i)2=-9;-4的平方根为±2i;如果x2=-7,那么x=±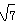 i.…数的不断发展进一步证实,这种规定是合理的.试用配方法求一元二次方程x2+x+1=0的非实数解:
i.…数的不断发展进一步证实,这种规定是合理的.试用配方法求一元二次方程x2+x+1=0的非实数解:  ,如果我们把x=2代入此多项式,发现多项式
,如果我们把x=2代入此多项式,发现多项式 =0,这时可以断定多项式中有因式(x-2)(注:把x=a代入多项式能使多项式的值为0,则多项式含有因式(x-a)),于是我们可以把多项式写成:
=0,这时可以断定多项式中有因式(x-2)(注:把x=a代入多项式能使多项式的值为0,则多项式含有因式(x-a)),于是我们可以把多项式写成: =
=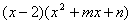 ,
,湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com