
题目列表(包括答案和解析)
宽与长的比是![]() 的矩形叫黄金矩形,心理学测试表明,黄金矩形令人赏心悦目,它给我们以协调,匀称的美感,现将同学们在教学活动中,折叠黄金矩形的方法归纳出以下作图步骤(如图所示):
的矩形叫黄金矩形,心理学测试表明,黄金矩形令人赏心悦目,它给我们以协调,匀称的美感,现将同学们在教学活动中,折叠黄金矩形的方法归纳出以下作图步骤(如图所示):
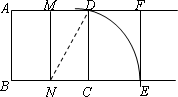
第一步:作一个任意正方形ABCD;
第二步:分别取AD,BC的中点M,N,连接MN;
第三步:以N为圆心,ND长为半径画弧,交BC的延长线于E;
第四步:过B作EF⊥AD交AD的延长线于F,
请你根据以上作法,证明矩形DCEF为黄金矩形,(可取AB=2)
课本中把长与宽之比为 的矩形纸片称为标准纸.请解决下列问题:
的矩形纸片称为标准纸.请解决下列问题:
(1)将一张标准纸ABCD(AB<BC)对开,如图1所示,所得的矩形纸片ABEF是标准纸.请给予证明;

(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:
第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图2甲);
第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图2乙) .此时E点恰好落在AE边上的点M处;
第三步:沿直线DM折叠(如图2丙),此时点G恰好与N点重合.

请你研究,矩形纸片ABCD是否是一张标准纸?请说明理由.
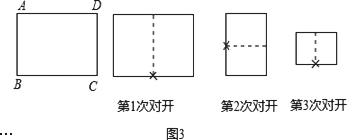
(3)不难发现,将一张标准纸如图3一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC= ,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2002次对开后所得标准纸的周长.
,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2002次对开后所得标准纸的周长.

 的矩形纸片称为标准纸.请解决下列问题:
的矩形纸片称为标准纸.请解决下列问题: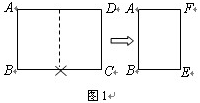

 ,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2002次对开后所得标准纸的周长.
,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2002次对开后所得标准纸的周长.
课本中把长与宽之比为![]() 的矩形纸片称为标准纸.请解决下列问题:
的矩形纸片称为标准纸.请解决下列问题:
(1)将一张标准纸ABCD(AB<B![]() C)对开,如图1所示,所得的矩形纸片ABEF是标准纸.请给予证明.
C)对开,如图1所示,所得的矩形纸片ABEF是标准纸.请给予证明.
![]() (2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:
(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:
第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图2甲);第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图2乙) .
此时E点恰好落在AE边上的点M处;
第三步:沿直线DM折叠(如图2丙),此时点G恰好与N点重合.
请你研究,矩形纸片ABCD是否是一张标准纸?请说明理由.
 (3)不难发
(3)不难发![]() 现,将一张标准纸如图3一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC=
现,将一张标准纸如图3一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC=![]() ,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2002次对开后所得标准纸的周长.
,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2002次对开后所得标准纸的周长.
课本中,把长与宽之比为![]() 的矩形纸片称为标准纸.请思考解决下列问题:
的矩形纸片称为标准纸.请思考解决下列问题:
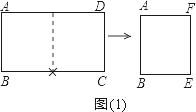
(1)将一张标准纸ABCD(AB<BC)对开,如图(1)所示,所得的矩形纸片ABEF是标准纸.请给予证明.
(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:
第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图(2)甲);
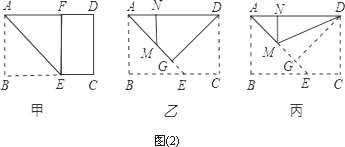
第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图(2)乙),此时E点恰好落在AE边上的点M处;
第三步:沿直线DM折叠(如图(2)丙),此时点G恰好与N点重合.
请你探究:矩形纸片ABCD是否是一张标准纸?请说明理由.
(3)不难发现:将一张标准纸按如图(3)一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC=![]() ,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.
,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com