练习册

  • 练习册
  • 试题
    如图:AB=DC.AC=BD.则图中的全等三角形有( )对 A.1 B.2 C.4 D.3 【查看更多】

     

    题目列表(包括答案和解析)

    为了测量一池塘的两端A，B之间的距离，同学们想出了如下的两种方案：

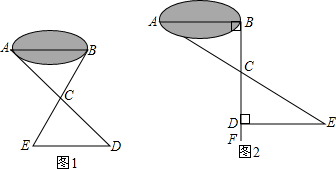
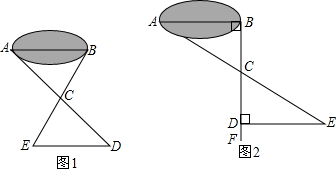
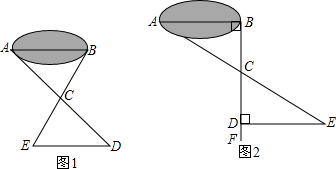
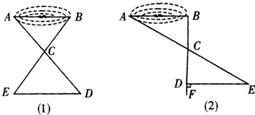
    ①如图1，先在平地上取一个可直接到达A，B的点C，再连接AC，BC，并分别延长AC至点D，BC至点E，使DC=AC，EC=BC，最后量出DE的距离就是AB的长；
    ②如图2，过点B作AB的垂线BF，在BF上取C，D两点，使BC=CD，接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即是AB的距离．
    问：
    （1）方案①是否可行？
    可行
    可行
    ，理由是
    SAS可证明△ACB≌△DCE，再根据全等三角形的性质可得AB=ED
    SAS可证明△ACB≌△DCE，再根据全等三角形的性质可得AB=ED
    ；
    （2）方案②是否可行？
    可行
    可行
    ，理由是
    ASA可证明△ACB≌△DCE，再根据全等三角形的性质可得AB=ED
    ASA可证明△ACB≌△DCE，再根据全等三角形的性质可得AB=ED
    ；
    （3）小明说在方案②中，并不一定需要BF⊥AB，DE⊥BF，只需要
    AB∥DE
    AB∥DE
    就可以了，请把小明所说的条件补上．

    查看答案和解析>>

    探究问题
    （1）方法感悟：
    一班同学到野外上数学活动课，为测量池塘两端A、B的距离，设计了如下方案：
    方案（Ⅰ）如图1，先在平地上取一个可直接到达A、B的点C，连接AC、BC，并分别延长AC至D，BC至E，使DC=AC，EC=BC，最后测出DE的距离即为AB的长；感悟解题方法，并完成下列填空：
    解：在如图所示的两个三角形△DEC和△ABC中：DC=AC，∠
    ACB
    ACB
    =∠
    DCE
    DCE
    （对顶角相等），EC=BC，∴△DEC≌△ABC
    （SAS）
    （SAS）
    ，∴DE=AB（全等三角形对应边相等），即DE的距离即为AB的长．
    （2）方法迁移：
    方案（Ⅱ）如图2，先过B点作AB的垂线BF，再在BF上取C、D两点使BC=CD，接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离．请你说明理由．  
    （3）问题拓展：
    方案（Ⅱ）中作BF⊥AB，ED⊥BF的目的是
    作∠ABC=∠EDC=90°
    作∠ABC=∠EDC=90°
    ；若仅满足∠ABD=∠BDE≠90°，方案（Ⅱ）是否成立？
    成立
    成立
    ．

    查看答案和解析>>

    探究问题
    （1）方法感悟：
    一班同学到野外上数学活动课，为测量池塘两端A、B的距离，设计了如下方案：
    方案（Ⅰ）如图1，先在平地上取一个可直接到达A、B的点C，连接AC、BC，并分别延长AC至D，BC至E，使DC=AC，EC=BC，最后测出DE的距离即为AB的长；感悟解题方法，并完成下列填空：
    解：在如图所示的两个三角形△DEC和△ABC中：DC=AC，∠______=∠______（对顶角相等），EC=BC，∴△DEC≌△ABC______，∴DE=AB（全等三角形对应边相等），即DE的距离即为AB的长．
    （2）方法迁移：
    方案（Ⅱ）如图2，先过B点作AB的垂线BF，再在BF上取C、D两点使BC=CD，接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离．请你说明理由．　
    （3）问题拓展：
    方案（Ⅱ）中作BF⊥AB，ED⊥BF的目的是______；若仅满足∠ABD=∠BDE≠90°，方案（Ⅱ）是否成立？______．

    查看答案和解析>>

    探究问题
    （1）方法感悟：
    一班同学到野外上数学活动课，为测量池塘两端A、B的距离，设计了如下方案：
    方案（Ⅰ）如图1，先在平地上取一个可直接到达A、B的点C，连接AC、BC，并分别延长AC至D，BC至E，使DC=AC，EC=BC，最后测出DE的距离即为AB的长；感悟解题方法，并完成下列填空：
    在如图所示的两个三角形△DEC和△ABC中：DC=AC，∠______=∠______（对顶角相等），EC=BC，∴△DEC≌△ABC______，∴DE=AB（全等三角形对应边相等），即DE的距离即为AB的长．
    （2）方法迁移：
    方案（Ⅱ）如图2，先过B点作AB的垂线BF，再在BF上取C、D两点使BC=CD，接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离．请你说明理由．  
    （3）问题拓展：
    方案（Ⅱ）中作BF⊥AB，ED⊥BF的目的是______；若仅满足∠ABD=∠BDE≠90°，方案（Ⅱ）是否成立？______．

    精英家教网

    查看答案和解析>>

    27、阅读理解：
    某校二（1）班学生到野外活动，为测量一池塘两端A，B的距离，设计出如下几种方案：
    （Ⅰ）如图先在平地取一个可直接到达A，B的点C，再连接AC，BC，并分别延长AC至D，BC至E，使DC=AC，EC=BC，最后测出DE的距离即为AB之长．
    （Ⅱ）如图（2），先过点B作AB的垂线BF，再在BF上取C，D两点，使BC=CD，接着过点D作BD的垂线DE，交AC的延长线于点E，则测出了DE的长即为A，B的距离．
    阅读后回答下列问题：
    （1）方案（Ⅰ）是否可行，理由是
    利用“边角边”判断两个三角形全等，对应边就相等．
    ．
    （2）方案（Ⅱ）是否可行，理由是
    利用“角边角”判断两个三角形全等，对应边就相等．
    ．
    （3）方案（Ⅱ）中作BF⊥AB，ED⊥BF的目的是
    对应角∠ABD=∠BDE=90°
    ，若仅满足∠ABD=∠BDE≠90°，方案（Ⅱ）是否成立？

    查看答案和解析>>


    同步练习册答案