
题目列表(包括答案和解析)
| ||
|
| A、4b | ||||
B、2
| ||||
C、
| ||||
D、
|
| x+y | ||
|
A、
| ||||
B、
| ||||
C、(x+y)
| ||||
| D、1 |
请同学们判断下列各式是否成立:
(1)![]() =2
=2![]() ;(2)
;(2)![]() =3
=3![]() ;(3)
;(3)![]() =4
=4![]() ;(4)
;(4)![]() =3
=3![]() .
.
经过计算可知,(1)、(2)、(3)式是成立的;(4)式是不成立的.这说明在二次根式的化简运算中要特别注意,根号里面的数是不能轻易地放到根号外面来的.
细心的同学可能会想,什么情况下根号里面的数能放到根号外面来呢?(1)、(2)、(3)式的成立仅仅是巧合吗?其中会有什么规律吧?我们来分析一下前三个式子的运算过程:
(1)![]() =
=![]() =
=![]() =2
=2![]() ;
;
(2)![]() =
=![]() =
=![]() =3
=3![]() ;
;
(3)![]() =
=![]() =
=![]() =4
=4![]() .
.
通过把带分数化成假分数的分数运算和分子开方运算验证了这些式子是成立的.
我们再来观察前三个等式左边根号内分数的特点.在三个带分数2![]() 、3
、3![]() 、4
、4![]() 中:
中:
(1)整数部分与分数部分的分子相等:
2=2,3=3,4=4;
(2)整数部分与分数部分的分母有下列关系:
3=22-1,8=32-1,15=42-1.
根据上面的分析和观察,我们不妨观察5+![]() =5
=5![]() ,式子
,式子![]() =5
=5![]() 是不是也成立?
是不是也成立?
![]() =
=![]() =
=![]() =5
=5![]()
确实是成立的!
大胆地猜想一下,对于一般的形式a+![]() (a为大于1的整数),式子
(a为大于1的整数),式子
![]() =a
=a![]()
还会成立吗?我们来验证一下:
![]() =
=![]() =
=![]()
=![]() =a
=a![]()
(a为大于1的整数).
太妙啦!我们的猜想是正确的.
那么,下列各式成立吗?
(1)![]() =2
=2![]() ;(2)
;(2)![]() =3
=3![]() ;(3)
;(3)![]() =4
=4![]() ;(4)
;(4)![]() =3
=3![]() .
.
能不能由此得出下面的结论呢?
![]() =a
=a![]()
同学们可能还会不满足,还会有更大胆的猜想!那就试试看吧.不要忘记,猜想成为真理,是要经过严格证明的.
阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意指两个人合在一起,取长补短,威力无比.在二次根式中也有这样相辅相成的例子.
如 ,
,
它们的积是有理数,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
如 ,
,
象这样,通过分子、分母同乘以一个式子把分母中的根号化去或根号中的分母化去,叫做分母有理化.
解决问题:
(1)  的有理化因式是 .
的有理化因式是 . 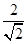 分母有理化得 .
分母有理化得 .
(2)分母有理化:(1)  ="_________;(2)"
="_________;(2)"  ="________;(3)"
="________;(3)" 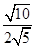 =______..
=______..
(3)计算:  .
.
阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意指两个人合在一起,取长补短,威力无比.在二次根式中也有这样相辅相成的例子.
如 ,
,
它们的积是有理数,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
如 ,
,
象这样,通过分子、分母同乘以一个式子把分母中的根号化去或根号中的分母化去,叫做分母有理化.
解决问题:
(1) 的有理化因式是 .
的有理化因式是 .  分母有理化得 .
分母有理化得 .
(2)分母有理化:(1)  ="_________;(2)"
="_________;(2)"  ="________;(3)"
="________;(3)"  =______..
=______..
(3)计算:  .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com