
题目列表(包括答案和解析)
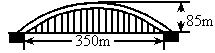
目前国内最大跨径的钢管混凝土拱桥--永和大桥,是南宁市又一标志性建筑,其拱形图形为抛物线的一部分(如图1),在正常情况下,位于水面上的桥拱跨度为350米,拱高为85米.
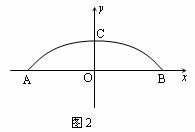
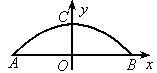
(1)在所给的直角坐标系中(如图2),假设抛物线的表达式为y=ax2+b,请你根据上述数据求出a、b的值,并写出抛物线的表达式(不要求写自变量的取值范围,a、b的值保留两个有效数字).

![]()
(2
)七月份汛期将要来临,当邕江水位上涨后,位于水面上的桥拱跨度将会减小,当水位上涨 4 m 时,位于水面上的桥拱跨度有多大?(结果保留整数).(2004 南宁)目前国内最大跨径的钢管混凝土拱桥——永和大桥,是南宁市又一标志性建筑,其拱形图形为抛物线的一部分(见图a),在正常情况下,位于水面上的桥拱跨度为350m,拱高为85m.
a)
(1)在所给的直角坐标系中(见图b),假设抛物线的表达式为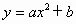 ,请你根据上述数据求出a、b的值,并写出抛物线的表达式(不要求写自变量的取值范围,a、b的值保留两个有效数字);
,请你根据上述数据求出a、b的值,并写出抛物线的表达式(不要求写自变量的取值范围,a、b的值保留两个有效数字);
b)
(2)七月份汛期将要来临,当邕江水位上涨后,位于水面上的桥拱跨度将会减小.当水位上涨4m时,位于水面上的桥拱跨度有多大?(结果保留整数)

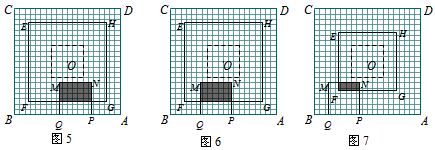
图1至图7的正方形霓虹灯广告牌ABCD都是20×20的等距网格(每个小方格的边长均为1个单位长),其对称中心为点O.
如图1,有一个边长为6个单位长的正方形EFGH的对称中心也是点O,它以每秒1个单位长的速度由起始位置向外扩大(即点O不动,正方形EFGH经过一秒由6×6扩大为8×8;再经过一秒,由8×8扩大为10×10;……),直到充满正方形ABCD,再以同样的速度逐步缩小到起始时的大小,然后一直不断地以同样速度再扩大、再缩小.
另有一个边长为6个单位长的正方形MNPQ从如图1所示的位置开始,以每秒1个单位长的速度,沿正方形ABCD的内侧边缘按A→B→C→D→A移动(即正方形MNPQ从点P与点A重合位置开始,先向左平移,当点Q与点B重合时,再向上平移,当点M与点C重合时,再向右平移,当点N与点D重合时,再向下平移,到达起始位置后仍继续按上述方式移动).
正方形EFGH和正方形MNPQ从如图1的位置同时开始运动,设运动时间为x秒,它们的重叠部分面积为y个平方单位.
(1)请你在图2和图3中分别画出x为2秒、18秒时,正方形EFGH和正方形MNPQ的位置及重叠部分(重叠部分用阴影表示),并分别写出重叠部分的面积;
(2)①如图4,当1≤x≤3.5时,求y与x的函数关系式;
②如图5,当3.5≤x≤7时,求y与x的函数关系式;
③如图6,当7≤x≤10.5时,求y与x的函数关系式;
④如图7,当10.5≤x≤13时,求y与x的函数关系式.
(3)对于正方形MNPQ在正方形ABCD各边上移动一周的过程,请你根据重叠部分面积y的变化情况,指出y取得最大值和最小值时,相对应的x的取值情况,并指出最大值和最小值分别是多少.(说明:问题(3)是额外加分题,加分幅度为1~4分)


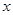 台,A、B两省将捐赠的挖掘机全部调往灾区共耗资
台,A、B两省将捐赠的挖掘机全部调往灾区共耗资 万元。
万元。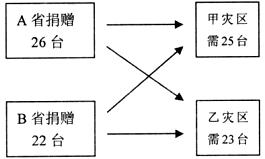
 与
与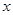 之间的函数关系式及自变量
之间的函数关系式及自变量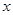 的取值范围;
的取值范围;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com